Slot machine outcomes are controlled by programs called pseudorandom number generators that produce baffling results by design. Government regulators, such as the Missouri Gaming Commission, vet the integrity of each algorithm before casinos can deploy it.
But as the “pseudo” in the name suggests, the numbers aren’t truly random. Because human beings create them using coded instructions, PRNGs can’t help but be a bit deterministic. (A true random number generator must be rooted in a phenomenon that is not manmade, such as radioactive decay.) PRNGs take an initial number, known as a seed, and then mash it together with various hidden and shifting inputs—the time from a machine’s internal clock, for example—in order to produce a result that appears impossible to forecast. But if hackers can identify the various ingredients in that mathematical stew, they can potentially predict a PRNG’s output.
- Brendan Koerner , “Russians Engineer a Brilliant Slot Machine Cheat—And Casinos Have No Fix”, Wired.com
Tilting At Windmills
Around 2007 I was working on an embedded Linux/GNU product. I was perusing the installation notes for GNU Privacy Guard, which was an open source implementation of the popular (at the time anyway) encryption software package Pretty Good Privacy (PGP). I had this crazy idea for a mechanism by which I could securely automate certain aspects of system maintenance on the laboratory prototypes on which we were developing by using encrypted shell scripts. (I eventually did an open source implementation of this which I wrote about in Automating Maintenance on Embedded Systems with Biscuits.)
The GnuPG README talked about the implications of choosing /dev/urandom versus /dev/random for acquiring random numbers with which to generate the encryption keys used by the software. I went off to read the random(4) manual page, after which I began to get the vague notion that I had no idea what I was doing. That realization launched me on a quest that I have been on for the better part of a decade now. And it led me owning what surely must be one of the world's greatest private collections of hardware entropy generators.
This article is the epic tale of that quest. And it expands on my talk John Sloan and Hardware Entropy Generators, a video of which is available on YouTube thanks to my good friends at Gogo Business Aviation.
Ancient History
Around 2007 I was working on an embedded Linux/GNU product. I was perusing the installation notes for GNU Privacy Guard, which was an open source implementation of the popular (at the time anyway) encryption software package Pretty Good Privacy (PGP). I had this crazy idea for a mechanism by which I could securely automate certain aspects of system maintenance on the laboratory prototypes on which we were developing by using encrypted shell scripts. (I eventually did an open source implementation of this which I wrote about in Automating Maintenance on Embedded Systems with Biscuits.)
The GnuPG README talked about the implications of choosing /dev/urandom versus /dev/random for acquiring random numbers with which to generate the encryption keys used by the software. I went off to read the random(4) manual page, after which I began to get the vague notion that I had no idea what I was doing. That realization launched me on a quest that I have been on for the better part of a decade now. And it led me owning what surely must be one of the world's greatest private collections of hardware entropy generators.
This article is the epic tale of that quest. And it expands on my talk John Sloan and Hardware Entropy Generators, a video of which is available on YouTube thanks to my good friends at Gogo Business Aviation.
Ancient History
If you were to read the manual page for rand(3), one of several random number generators available in the standard C library, you would find two functions as part of that API.
void srand(unsigned int seed);
int rand(void);
The srand function is used to initialize the random number generator with a seed, after which the rand function returns a different "random" number upon every subsequent call.
I write "random" because there was actually nothing random about it. If you initialize the generator by calling srand with exactly the same value for the seed, you will get exactly the same sequence of integer numbers with every call to rand.
In fact, not only will the same seed yield the same sequence of numbers from the generator, the sequence would eventually start to repeat, if you made enough calls to rand. It would take a lot of calls. But still.
So here's the thing: there is no randomness in the standard C - or indeed any - random number generator algorithm. The randomness, if there is any, comes from the value you choose for the seed.
It has to work this way, because there is nothing random about digital computer systems. We work really hard to eliminate any randomness, or non-determinism, from them. Determinism, or predictability, is a good thing. For the most part. Usually.
The period of the repeating cycle is also completely deterministic. If the random number generator has an internal state of N bits, than its output can have a period of no more than 2N values - and sometimes a lot less - after which it will begin to repeat. This is an inevitable result from information theory. But if you think about it, the algorithm, which is a kind of state machine, has to work this way. When there is no source of external stimulus, the same input - its internal state - yields the same output.
So if you were to see a long enough - perhaps a very, very, very long - sequence of values from a particular random number generator, it might be possible - expensive, but possible - for you to identify that sequence just from its pattern, correlate it with a particular seed value, and then predict what every single subsequent value from that random number generator would be.
That's why the people that actually worry about these things call these algorithms pseudo random number generators (PRNGs). So if you want truly random results, you have to figure out some way to introduce it using a random seed value. It is the seed that contains all the randomness, or unpredictability, or what information theorists, borrowing a term from thermodynamics, call entropy.
So here's the thing: there is no randomness in the standard C - or indeed any - random number generator algorithm. The randomness, if there is any, comes from the value you choose for the seed.
It has to work this way, because there is nothing random about digital computer systems. We work really hard to eliminate any randomness, or non-determinism, from them. Determinism, or predictability, is a good thing. For the most part. Usually.
The period of the repeating cycle is also completely deterministic. If the random number generator has an internal state of N bits, than its output can have a period of no more than 2N values - and sometimes a lot less - after which it will begin to repeat. This is an inevitable result from information theory. But if you think about it, the algorithm, which is a kind of state machine, has to work this way. When there is no source of external stimulus, the same input - its internal state - yields the same output.
So if you were to see a long enough - perhaps a very, very, very long - sequence of values from a particular random number generator, it might be possible - expensive, but possible - for you to identify that sequence just from its pattern, correlate it with a particular seed value, and then predict what every single subsequent value from that random number generator would be.
That's why the people that actually worry about these things call these algorithms pseudo random number generators (PRNGs). So if you want truly random results, you have to figure out some way to introduce it using a random seed value. It is the seed that contains all the randomness, or unpredictability, or what information theorists, borrowing a term from thermodynamics, call entropy.
The rand(3) API has a long history. Way back in 1977 I was writing simulation code in Fortran IV for an IBM mainframe. The random number generator in the standard Fortran IV library had the same two functions with the same names, albeit in upper case of course (I don't think punch card machines even had a shift key): SRAND and RAND. And I got the bright idea of using the value of the mainframe's Time Of Day (TOD) hardware clock as the seed. Today, when I write simulations for a UNIX system, I might use the value returned by time(2), the system call that returns the number of seconds since the start of the UNIX epoch, as the seed to rand(3). Of course, that means if someone knew exactly when I ran my simulation, they could guess my seed. But for simulation code that needs to have different results every time it is run, it works pretty well.
Roll On Big O
If you think about the properties you want in an encryption algorithm, the one right at the top of the list would be: you want it to be computationally cheap to encrypt and decrypt, but almost impossible to brute force decrypt. Functions that are easy in one direction but almost impossible in another are called trapdoor functions, or sometimes one-way functions.
A good example of a trapdoor function is multiplying two big numbers together, then trying to brute force deduce what those original two numbers were by factoring the product into its prime factors. It turns out that if the two numbers were N bits long, then multiplying them together (or dividing the product by either original number) takes an amount of work proportional to N2, or O(N2) in "big O" notation. But factoring the resulting product into its prime factors and trying every combination of all those prime factors to reproduce the original two numbers proportionately takes O(2N) work.
We can make a little table showing how the amount of work for factoring relative to multiplying grows as N gets larger.
We can make a little table showing how the amount of work for factoring relative to multiplying grows as N gets larger.
The log10 columns tell you how many decimal digits are in the results, which is just a quick way to see the magnitude of those values. So if you were to multiply two 512 bit numbers together, the work involved would be proportional to a value more then five digits long. But if you were to brute force try to recover the original two numbers from their product, it would take an amount of work proportional to a value that is more than one hundred and fifty four digits in length.
Just to make this clear: brute force factoring for numbers eight bits long is 256/64 or four times as expensive than multiplication or division; for numbers 512 bits long it is within shouting distance of 10148 times more expensive than the original multiplication or division operation. That value is a 1 followed by one hundred and forty-eight zeros, a number so astoundingly big we don't have a word for it, but it is a lot larger than the estimated number of hydrogen atoms in the universe. (corrected 2017-03-03)
If it's not obvious what's going on, here is a graph of the log10 columns.
Just to make this clear: brute force factoring for numbers eight bits long is 256/64 or four times as expensive than multiplication or division; for numbers 512 bits long it is within shouting distance of 10148 times more expensive than the original multiplication or division operation. That value is a 1 followed by one hundred and forty-eight zeros, a number so astoundingly big we don't have a word for it, but it is a lot larger than the estimated number of hydrogen atoms in the universe. (corrected 2017-03-03)
If it's not obvious what's going on, here is a graph of the log10 columns.
Keep in mind that we're graphing the logarithm of the values. Otherwise the 2N graph would increase so quickly it would be unusable. The growth of the work required for multiply and divide is said to be polynomial. But the growth of the work for factoring is exponential, which grows far far faster.
You could be forgiven if the thought occurred to you: hey, if we could just encrypt a message by multiplying it by a secret key (the message and the key being just numbers inside a computer), and decrypt the encrypted message by dividing it by that same secret key, the bad guys would find it almost impossible to brute force decrypt our encrypted message.
And that's exactly what happens.
It is obvious now that the security of your encryption mechanism all revolves around keeping your secret key secret. If the bad guy has your secret key, you might as well be publishing your secret messages on Facebook.
You have to choose a secret key that the bad guy isn't likely to guess. Your birthday, or your mobile phone number, and what not, is a really bad idea.
And you have to have some secure way to communicate your secret key to the person who is to receive your encrypted messages. If the bad guy taps your communication channel and reads your secret key, he has the means to trivially break your encryption.
You also need a lot of secret keys. Every time you click on a web link whose Uniform Resource Locator (URL) uses the https protocol, like in https://www.google.com - the s standing for "secure" - you need a new secret key with which to encrypt the data going to the web server and coming back to your web browser.
So what your web browser does is it generates a new secret key for every such transaction, and it does so in a way that the bad guy is not likely to guess: it generates a random number to use as the key.
And now we are on a mission to find a good seed.
The random Device Driver
If the option CONFIG_ARCH_RANDOM was enabled when the Linux kernel was configured and built, there is a device driver that generates random numbers. An application can acquire random numbers just by doing a read(2) against this driver. The driver exposes two interfaces in the /dev device directory: /dev/random and /dev/urandom. The random(4) manual page distinguishes between the two interfaces by telling us that /dev/random blocks (makes the application wait on the read) if the available entropy in the driver is exhausted, while /dev/urandom endlessly delivers as many values as the application cares to read. This raises the obvious question as to what exactly is /dev/urandom is returning if /dev/random is blocked because entropy is exhausted? And where does that entropy come from?
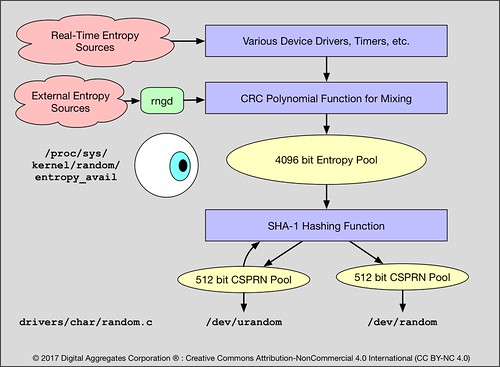
We can find the source code for this driver in drivers/char/random.c in the kernel source tree (3.10.105 is the version I perused). It's not that big. We'll start at the application interface and work backwards to discover where these random numbers from from.
/dev/urandom and /dev/random each have their own 512 bit pool that is used to store Cryptographically Secure Pseudo Random Numbers (CSPRNs). "Cryptographically Secure" means the random numbers are of high enough quality to be useful for cryptography, that is, for encryption. "Pseudo" is our first clue that they are the result of a pseudo-random number generator algorithm.
And indeed they are: they are generated by SHA-1, a well known cryptographic hash algorithm invented by the U. S. National Security Agency (NSA). SHA-1 takes an input - a seed - of any size and outputs a 160 bit number or cryptographic hash value. This hash value is said to be "cryptographic" because (you guessed it) it has properties useful for cryptography, one of the main ones being that given a SHA-1 hash value it is so expensive to try to brute force recover the original input value as to be computationally infeasible.
We have enough background now to know that the quality of the random numbers from this driver must depend on [1] the quality of the entropy being fed as a seed to SHA-1 for either /dev/random or /dev/urandom, and [2] the period of the SHA-1 algorithm when it gets used iteratively by /dev/urandom.
Note that there is still no source of entropy here. SHA-1 is a deterministic algorithm.
The SHA-1 function takes its input from a 4096 bit pool of entropy. The bits stored in this pool, no matter from whence they came, flow through a Cyclic Redundancy Check (CRC) polynomial that is used to merely mix bits from different entropy sources together, rendering the bits stored in the entropy pool anonymous, that is, unidentifiable as to their origin or meaning. This prevents a bad guy from learning anything useful about the internal state of the system from perusing the contents of this entropy pool.
Nope, still no source of entropy. The CRC is completely deterministic.
When the driver blocks a read on /dev/random, it is not measuring entropy based on the number of bits in either the 512 bit CSPRN pool used by /dev/random, nor on the number of bits in the 4096 bit entropy pool that feeds the SHA-1 algorithm. They are not that kind of First In First Out (FIFO) pools. Instead the driver tries to measure the effective randomness of the bits flowing into the CRC. It does this by measuring the first and second derivatives of the values for each of the entropy sources feeding the CRC.
This sounds a lot more high falutin' than it is. The driver merely looks to see if the difference between successive values of the original entropy data is changing (the first derivative), and if the difference between successive values of the first derivative is changing (the second derivative). From these values that are the result of simple subtractions, it computes an approximate measure of the entropy, or amount of randomness, in the data feeding the entropy pool. It is when this measure reaches zero that the behavior of both /dev/random and /dev/urandom changes.
You can read this measure of entropy but just looking at the value of the /proc file system entry /proc/sys/kernel/random/entropy_avail. You can do this from the command line by just using the cat command. But if you do so, you'll notice something interesting: every time you run the command, the amount of entropy is reduced!
This is because the kernel itself is a consumer of entropy, even if the entropy is not being used to generate encryption keys. The Linux kernel implements a feature called Address Space Layout Randomization (ASLR). Whenever the kernel dynamically allocates memory, including to run processes like the cat command, it reads bits from /dev/urandom to use to randomize where in the virtual memory address space the allocated memory block is placed.
This makes it much more difficult for the bad guy to attack the kernel by, for example, using kernel exploits - also known as bugs - to deliberately fool the kernel into overflowing buffers, resulting in overwriting other kernel data structures or even executable instructions.
As result, the pool of available entropy in the kernel driver is continuously being consumed.
So exactly where is the entropy in the kernel random driver coming from? As I mentioned before, digital computer systems kinda suck by design at non-determinacy. So entropy in Linux comes from natural sources of non-determinism: measured latencies of physical I/O devices like spinning disks; activity by users of human interface devices (HID) like keyboards and mice; inter arrival time of network packets and interrupts; variation in the firing of timers; and other sources of unpredictable behavior.
The random driver contains a kernel API by which other device drivers in the system can report these values and add them to the entropy pool. You can find calls to this API littered throughout the Linux kernel. Here are some to look for, using your favorite source code browser.
I came to realize that there was almost no non-determinacy in the system. My product spent most of its time with little or no entropy. Which meant that /dev/random was effectively unusable, and the quality of the random numbers from /dev/urandom kinda sucked.
I realized that this could be a issue with all embedded Linux systems. Over time, I was to discover that this situation was hardly unique to me, or even to embedded systems.
Virtual machines running Linux - the backbone of cloud based computing - frequently ran short of usable entropy, because their I/O devices were for the most part nothing more than software abstractions on top of the system on which they ran, and which exhibited little or no random behavior.
And even an honest to goodness actual Linux server may have little or no entropy available when it first boots up, which is exactly when it may be establishing secure socket layer (SSL) connections to other servers, long lived connections that were made using poor quality seeds to their encryption algorithms.
What we needed was a reliable source of true entropy that could be easily integrated into products built around the Linux/GNU stack, a source that would not rely on largely hypothetical non-determinancy.
Note that the implementation of /dev/random and /dev/urandom are virtually identical. Both deliver random bits from the same entropy pool, filled from the same entropy sources, mixed with the same CRC polynomial, and conditioned by the same SHA-1 algorithm. The only difference is what they do when the estimated entropy in the driver is exhausted. So the answer to my original question back in 2007 about whether to use /dev/random or /dev/urandom is:
There are a number of physical processes that exhibit behavior that is effectively unpredictable and which can be digitized. These sources of entropy can be broadly divided into two categories: quantum or classical.
Quantum entropy sources are, as far as we know today, wired right into the physical nature of reality. Our current understanding of physics leads us to believe that there is no way to externally influence such entropy sources. Examples of quantum entropy include whether a photon passes through or is reflected by a partially silvered mirror; when a radioactive particle decays; when an electron tunnels through the band gap of a transistor to its base; when a photon falls on a photodiode and creates an electrical current.
Classic entropy sources may be said to be more chaotic than random, that is, influenced by environmental factors that are typically beyond our control. Examples of classic entropy include thermal noise from a resistor; electronic noise from an avalanche diode or from a zener diode in breakdown; atmospheric noise from a radio receiver; analog/digital convertor noise. These are all noise sources that a competent electrical engineer would normally work hard to eliminate in any design.
Each of these entropy sources can be amplified, instrumented, and digitized to produce a string of ones and zeros. However, even though they are unpredictable processes, such processes may not be unbiased: they may be more likely to produce ones or zeros. The bias can occur from practically unmeasureable variations in materials, or from minuscule differences in the sampling rate of the digitization, so that even in a modern semiconductor fabrication process, successive devices may yield very slightly different results.
A simple algorithm for whitening the bit stream - turning it into true white noise where ones and zeros occur with equal probability - is a problem solved long ago by none other than mathematician, computer scientist, information theorist, and Cold War strategist John von Neumann.
Every hardware entropy generator consists of (at least) three stages: a hardware process that generates true entropy, a stage that digitizes the entropy into a stream of ones and zeros, and a whitening stage that conditions the binary stream into white noise. These stages are typically implemented in hardware, or microcontroller firmware, embedded inside the hardware entropy generator.
Testing Entropy in the Short Run
For hardware entropy generators destined for use in applications which must conform to U.S. Federal Information Processing Standards (FIPS), which include not just U.S. government systems, or systems used by U.S. government contractors, but also commercial companies or regional agencies who just think such conformance is a good idea (or, as it turns out, manufacturers of electronic games of chance destined for gambling casinos that don't want to be ripped off), the U. S. National Institute of Standards and Technology (NIST) defines a set of statistical tests, FIPS 140-2, to be continuously run on the output of such generators to insure that they remain unbiased and have not failed in some non-obvious way. This is a fourth stage of such generators.
Some of the generators I have tested implement these FIPS tests themselves, but most take advantage of the rngd(8) user space daemon that is part of the rng-tools package available for most Linux/GNU distributions. rngd implements these tests in software against any hardware entropy generator for which it is configured to extract entropy to be injected via ioctl into the random device driver.
For most of the hardware entropy generators that I have tested, it is a very simple matter to integrate them into the system using rngd: usually a matter of installing the rng-tools package, doing some minor editing to the configuration file /etc/default/rng-tools, and sometimes a little udev rule hacking so that the generator shows up as a serial device in /dev.
Verifying Entropy in the Long Run
In addition to the FIPS tests, which are fast enough to be done in real-time, several folks who are interested in such things have developed suites of tests to be run against hardware entropy generators, and pseudo random number generators in general, to verify their broad long-term statistical properties. Each of these tests or suites of tests consume anywhere from kilobytes to terabytes of random bits, and require anywhere from seconds to weeks to run, even on a fast processor with a high-speed interface to the generator.
Scattergun is the code-name for my project to test consumer-grade hardware entropy generators and some software pseudo random number generators. It consists of the test script scattergun.sh, a Makefile to drive it, and a smattering of supporting software required to use the dozen or so generators that I own. (The supporting software included in Scattergun might be really useful to anyone using the more exotic generators, independent of the test script.) Scattergun is open source and can be found on GitHub. The raw results of all the testing are part of that repository as well. A link to the repository can be found near the end of this article.
Here is a brief description of the tests that the Scattergun script runs. The Scattergun script runs all of them, serially, accessing the hardware random number generator directly, without requiring that the generator be integrated into the system.
rngtest. Like rngd, rngtest is installed as part of the rng-tools package. It splits out the FIPS 140-2 tests that rngd runs in real-time into a command line tool where they can be run on demand. If a generator can't pass rngtest, it's not going to integrate into the system using rngd.
bitmap. This clever test ("clever" because I didn't think of it) exploits the ability of the human eyes and brain to perceive patterns in complex data. It extracts sufficient bits from a hardware entropy generator to create a 256 x 256 pixel Portable Network Graphics (PNG) file in 8-bit color. A successful generator should produce a PNG file that, in the words of one of my favorite authors William Gibson, "is the color of television, tuned to a dead channel". It is interesting to compare PNG files from various entropy sources and realize you can detect that the source only produces, for example, positive numbers because the most significant bit in each number being zero creates a distinct pattern, or it limits the dynamic range of values in some way that creates higher contrast colors.

This bitmap is from the hardware random number generator built into the Broadcom chip used on the Raspberry Pi 3.

This bitmap is from the random(3) C function that produces positive long integers.

This bitmap is from the mrand48(3) C function that produces positive and negative long integers.
ent. This is a quick "pseudorandom number sequence test program" written by John Walker. Some Linux/GNU distributions provide ent as an installable package. For those that don't, it can be easily downloaded from his web site, built, and installed. I like ent because it quickly provides an estimate of the effective entropy per byte, e.g. 7.999958 bits.
SP800-90B. This is a large suite of tests written in Python, developed by NIST, and made available on GitHub. It takes one or more hours to run on the typical generator. During this long duration side project, the repo on GitHub has been occasionally updated, so the SP800-90B tests have evolved as I've been using it. Since this suite is a NIST standard, its results probably carry more weight in certain circles.
dieharder. This is an enormous suite of tests developed by Robert Brown, a physicist at Duke University. Its name was inspired by the earlier diehard suite of statistical tests developed by George Marsaglia (and of course the Bruce Willis movie franchise). This dieharder suite consumes about a terabyte of entropy and can run for days or even weeks, depending on the speed of the hardware entropy generator, the interface to it, and the processor on which the test is running. It even drove one of the generators (OneRNG) I tested into failure due to overheating. I like that about it.
If you examine the results of these tests in the Scattergun GitHub repo, you will notice that some of the tests identify the generator as "weak", and some tests may even fail. This is not unusual. Statistically speaking, a sequence of numbers that doesn't look random is just as likely to be generated as any other sequence, so an occasional poor result is to be expected. It is when a lot of tests fail that you need to be concerned.
Shapes and Sizes (added 2017-03-03)
Hardware devices that generate true entropy, no matter what physical process they use to do so, come in a lot of shapes and sizes, with a variety of interfaces and features. Most of these can be integrated into your Linux/GNU system using the rngd(8) user space daemon from the rng-tools package. Some are already built right into the random(4) driver and just require the correct kernel configuration option (which may already be there).
External devices. Most of the generators I tested are external devices that connect to the host computer via the Universal Serial Bus (USB). Even so, there was a wide variety of software interfaces to these devices. The easiest enumerate as a serial port, typically requiring some minor udev rule hacking, and were trivial to use by just reading random bits from the port (TrueRNG2, TrueRNG3, TrueRNGpro, FST-01/NeuG). Some enumerated as a serial port, but required software to write commands to that port to initialize the device (OneRNGs). Some USB generators required a vendor-provided user-space utility to read from them (BitBabblers). One required a substantial software development effort (that I've done for you, yay!) using a vendor-provided library (Quantis).
Internal devices. The OneRNG comes in a form factor made to attach to an internal USB connector now present (as I was to learn) on many motherboards.
Internal cards. I didn't test it, but the the Quantis is available in a version with multiple entropy sources on a PCI-bus card.
Motherboard components. Although I didn't test it, Apple iPhones that use the A7 processor (the iPhone 5S and later) have a co-processor called the Secure Enclave Processor (SEP). The SEP has its own ARM core and has as a peripheral a hardware entropy generator. This generator is used to seed the encryption used by the iPhone.
Many personal computers intended for the enterprise or government markets include a Trusted Platform Module (TPM). The TPM, an industry standard created by the Trusted Computing Group (TCG), and examples of which are manufactured by several vendors, is similar in function to the SEP, and includes a hardware entropy generator. Even if you don't use the other features of the TPM, you can easily incorporate the TPM's generator into your Linux/GNU system as an entropy source. I've tested TPMs from two different vendors, in a laptop and in a server, belonging to one of my clients. Because that work was covered under non-disclosure, I don't include those results here. But you may have a TPM with a hardware entropy generator on your system already.
(Updated 2017-07-20) I now have a server that incorporates a TPM chip and I've added a test of its hardware entropy generator.
System peripherals. Some System on a Chips (SoC) feature entropy generators as a built-in peripheral. The Broadcom SoC used by the Raspberry Pi 2 and 3 boards (I haven't tested the Raspberry Pi 1) have such a peripheral. It's not enabled by default, but it's easy to do so by just loading the appropriate device driver module and using rngd(8).
Machine instructions. Recent Intel processors have implemented a hardware entropy source, and a PRNG that is automatically periodically reseeded by that source, as machine instructions: rdseed (Broadwell family) and rdrand (Ivy Bridge family) respectively. Latest versions of the Linux kernel destined for these processors automatically make use of rdrand to augment the legacy entropy sources in the random device driver.
Remarkably, there are a lot of hardware entropy generators on the market. Making an informed decision as to which one you want to use requires that you consider what your priorities are. It is a surprisingly multi-dimensional decision matrix.
Correctness. This is the easy one. I'll just jump right to the punch line and tell you that all of the hardware entropy generators that completed the Scattergun script did fine. One device failed during testing, and a new version (said to be more tolerant of heating) will start testing soon. Another is being tested now, and looks good. I noted the number of entropy bits (relative to eight bits) reported by ent, and the minimum entropy (ditto) reported by SP800-90B for its Independent and Identically Distributed (IID) test.
Price. For hardware entropy generators, I've paid as little as US$50 and as much as US$1100 (definitely an outlier on the price axis). There is no correctness difference, and not as much performance difference as you might expect, between the far ends of that range. You may be able to purchase a perfectly adequate hardware entropy generator for, if not lunch money, at least good dinner money, depending on what your other priorities are.
Acquisition. One of my generators I purchased by clicking the one-click ordering button on Amazon.com, had US$50 or so deducted off my credit card, and thanks to Amazon Prime had the device delivered to my front door in a couple of days. For others, I had to exchange encrypted email, send FAXes to Australia, and then wait for a shipment from China. All of the other devices fall somewhere on that range of effort to acquire.
Performance. The performance measurements should probably be taken with at least a small grain of salt, since there were a number of buffers between the actual device and the test suite. Even so, there is probably some merit in comparing the numbers. There was a fair amount of performance difference, in terms of entropy bits per second, among the generators. Some of the generators are peripherals built into an SoC (Raspberry Pi 2 and 3). Some are machine instructions built directly into the processor (rdrand and rdseed). Most are external USB devices. There was little correlation between the price of the device and its performance. But the interface typically made a difference. As you would expect, generally the internal devices performed better. But the best performer was an US$40 device with a USB interface (Chaos Key); the second best was the US$1100 device that also interfaced by USB (Quantis); the third place performer was a US$99 USB device (TrueRNGpro).
Robustness. One of the devices (OneRNG) failed during testing, probably due to overheating, which was a common complaint by users of this device. The vendor is now shipping a new version that I have received but have not tested yet. None of the other devices failed during testing, although I did manage to destroy one (OneRNG) designed for an internal USB connection on a motherboard, by hooking it up incorrectly.
Integration. Some of these devices were trivial to integrate into the system, requiring at most just a little udev hacking to get their USB interface recognized as a serial device. Some required use of a vendor-supplied user-space daemon or script (OneRNG, BitBabbler). And some (Quantis) required a substantial effort in software development using a vendor-supplied library; it's performance might be worth it.
Mechanism. Most of the hardware entropy generators use one of the cost effective mechanisms based on solid state electronics to generate entropy. Some have multiple entropy sources of different types which were mixed together. Some have multiple entropy sources of the same type used in parallel for more performance. And the Quantis has a beam splitter: a semiconductor photon emitter aimed at a photon detector behind a partially silvered mirror, for full on Heisenberg quantum uncertainty multiverse action. There probably are reasons why organizations that have an unusual sensitivity to the unimpeachability of their random numbers might use such a device.
Openness. This is one domain where it may pay to be a foil-hat-wearing member of the conspiracy theory club. Some of the devices were completely open, their firmware source code and hardware schematics published by the vendor. Most were completely closed and proprietary. Some of them (TrueRNG2, TrueRNG3, TrueRNGpro) were designed by folks within commuting distance of the headquarters of the National Security Agency; this is probably not a coincidence: that neck of the woods would tend to attract engineers who know how to design stuff like this. You'll have to decide how paranoid you are about these kinds of things.
Hardware Entropy Generators I Have Known (updated 2017-04-23)
Here is a rundown of the hardware entropy generators that I own, listed in the order that I tested them. Or am testing them. Or will be testing them.
Unfortunately, the Scattergun script doesn't lend itself to precise performance measurements since the script is fed data from the device through a UNIX pipe. Never the less, I did note the speed at which random bits were consumed from the pipe, figuring that over large amounts of data it would even out to more or less match the rate at which data was introduced into the pipe. All speeds are in kilobits or megabits per second.

TrueRNGpro (right).
Vendor: ublt.it (U.S.).
Correctness: 7.999958 entropy bits per byte, 7.94464 minimum entropy bits per byte.
Price: US$99.
Acquisition: easy.
Performance: 3.2Mbps claimed, 3.4Mbps measured.
Robustness: high.
Integration: easy (USB) (and the LEDs are comforting too).
Mechanism: semiconductor avalanche effect (two parallel sources).
Openness: closed.
Source: http://ubld.it/products/truerngpro

Quantis-USB-4M (left).
Vendor: ID Quantique (Switzerland).
Correctness: 7.999962 entropy bits per byte, 7.94601 minimum entropy bits per byte.
Price: US$1100 (E990).
Acquisition: medium.
Performance: 4Mbps claimed, 3.9Mbps measured.
Robustness: high.
Integration: difficult (USB but requires software development using vendor library).
Mechanism: beam splitter with photon counter (quantum effect).
Openness: closed.
Source: http://www.idquantique.com/random-number-generation/quantis-random-number-generator/

Raspberry Pi 2 (32-bit) BCM2708 HWRNG.
Vendor: Broadcom (BCM2836 SoC).
Correctness: 7.999954 entropy bits per byte, 7.94918 minimum entropy bits per byte.
Price: US$35 (Raspberry Pi 2).
Acquisition: easy.
Performance: 824Kbps measured.
Robustness: high.
Integration: easy (device driver).
Mechanism: undocumented.
Openness: open software, closed hardware.
Source: https://www.raspberrypi.org/products/raspberry-pi-2-model-b/

FST-01 NeuG.
Vendor: Flying Stone Technology via GNU Press (Free Software Foundation).
Correctness: 7.999959 entropy bits per byte, 7.94114 minimum entropy bits per byte.
Price: US$50.
Acquisition: easy.
Performance: 602 Kbps claimed, 653 Kbps measured.
Robustness: high.
Integration: easy (USB).
Mechanism: analog/digital convertor noise.
Openness: open (both software and hardware).
Source: https://shop.fsf.org/storage-devices/neug-usb-true-random-number-generator

rrand (machine instruction in the Ivy Bridge processor family and later).
Vendor: Intel (i7-6700T in my test).
Correctness: 7.999957 entropy bits per byte, 7.94404 minimum entropy bits per byte.
Price: N/A.
Acquisition: N/A.
Performance: 1600Mbps claimed, 228Mbps measured.
Robustness: high.
Integration: easy (integrated into random device driver in later Linux kernels).
Mechanism: AES PRNG periodically reseeded by the rdseed mechanism (see below).
Openness: open software, closed hardware.
Source: https://software.intel.com/en-us/articles/intel-digital-random-number-generator-drng-software-implementation-guide
rdseed (machine instruction in the Broadwell processor family and later).
Vendor: Intel (i7-6700T in my test).
Correctness: 7.999958 entropy bits per byte, 7.9408 minimum entropy bits per byte.
Price: N/A.
Acquisition: N/A.
Performance: 3.5 Mbps measured.
Robustness: high.
Integration: easy (integrated into random device driver in later Linux kernels).
Mechanism: thermal noise.
Openness: open software, closed hardware.
Source: https://software.intel.com/en-us/articles/intel-digital-random-number-generator-drng-software-implementation-guide
WEC TPM TCG 1.2 FW 5.81
Vendor: Winbond Electronics Corporation.
Correctness: TBD.
Price: N/A (embedded inside a Dell OptiPlex 7040 Micro Form Factor BTX desktop PC).
Acquisition: N/A.
Performance: TBD but not good. As of 2018-08-10 I've been running the Scattergun test suite against this Trusted Platform Module, embedded as a feature inside one of my otherwise unused Linux servers, for over a year. And while it continues to make progress, albeit very slowly, I don't have a projection of when it will finish. Clearly something is seriously amiss, since it made progress more quickly at the beginning. I'm limited as to the diagnostics I can run without interfering, or worse inadvertently interrupting, the test. But I don't see any errors in the log, as the suite continues to extract entropy from the /dev/hwrng device that exposes the TPM's entropy generator. I'll have to start looking much more closely at the tpm-rng kernel model to see how it's implemented. Update 2022-02-03: After four years and five months of running Scattergun against this device, my lab lost power - due to the same high winds that propagated the tragic Marshall fire across Boulder County on 2021-12-28 - long enough that the UPS powering this system finally ran dry. At the moment it failed, it was near the end of the last test suite in the Scattergun meta-suite. But saying it was "near the end" really means nothing. It continued to make slow progress, but could have run for several more years. Again, I'm assuming there was a problem somewhere in the test setup.
Robustness: TBD.
Integration: easy (loading tpm-rng kernel module exposes /dev/hwrng).
Mechanism: N/A.
Openness: open software, apparently closed firmware and hardware.
Source: N/A.

Raspberry Pi 3 (64-bit) BCM2708 HWRNG.
Vendor: Broadcom (BCM2837 SoC).
Correctness: 7.999956 entropy bits per byte, 7.9334 minimum entropy bits per byte.
Price: US$35 (Raspberry Pi 3).
Acquisition: easy.
Performance: 1Mbps measured.
Robustness: high.
Integration: easy (device driver).
Mechanism: undocumented.
Openness: open software, closed hardware.
Source: https://www.raspberrypi.org/products/raspberry-pi-3-model-b/

TrueRNG v2.
Vendor: ublt.it (U.S.).
Correctness: 7.999958 entropy bits per byte, 7.94464 minimum entropy bits per byte.
Price: US$50.
Acquisition: easy.
Performance: 350 Kbps claimed, 367 Kbps measured.
Robustness: high.
Integration: easy (USB).
Mechanism: semiconductor avalanche effect.
Openness: closed.
Source: http://ubld.it/products/truerng-hardware-random-number-generator/

OneRNG V2.0 External.
Vendor: Moonbase Otago (New Zealand).
Correctness: N/A.
Price: US$40.
Acquisition: medium (takes a while).
Performance: 350 Kbps claimed.
Robustness: failed during testing (overheating a common complaint, may be fixed in V3.0).
Integration: medium (USB but requires some initialization).
Mechanism: semiconductor avalanche effect and atmospheric noise.
Openness: open (both hardware and software).
Source: http://onerng.info

OneRNG v2.0 Internal.
Vendor: Moonbase Otago (New Zealand).
Correctness: N/A.
Price: US$40.
Acquisition: medium (takes a while).
Performance: 350 Kbps claimed.
Robustness: I managed to fry my one unit by hooking the internal USB cable up incorrectly.
Integration: medium (internal USB but requires some initialization).
Mechanism: semiconductor avalanche effect and atmospheric noise.
Openness: open (both hardware and software).
Source: http://onerng.info

BitBabbler White (bottom).
Vendor: VoiceTronix Pty. Ltd. (Australia).
Correctness: 7.999951 entropy bits per byte, 7.94498 minimum entropy bits per byte.
Price: AUS$199.
Acquisition: difficult (required a fair amount of effort).
Performance: 2.5 Mbps claimed, 1.2 Mbps measured.
Robustness: high.
Integration: medium (USB but requires vendor supplied user-space daemon).
Mechanism: shot noise, Johnson-Nyquist noise, flicker noise, RF noise (multiple sources).
Openness: open software and hardware.
Source: http://bitbabbler.org
BitBabbler Black (top).
Vendor: VoiceTronix Pty. Ltd. (Australia).
Correctness: 7.999963 entropy bits per byte, 7.93873 minimum entropy bits per byte.
Price: AUS$49.
Acquisition: difficult (required a fair amount of effort).
Performance: 625 Kbps claimed, 307 Kbps measured.
Robustness: high.
Integration: medium (USB but requires vendor supplied user-space daemon).
Mechanism: shot noise, Johnson-Nyquist noise, flicker noise, RF noise.
Openness: open software and hardware.
Source: http://bitbabbler.org

TrueRNG v3.
Vendor: ublt.it (U.S.).
Correctness: 7.999956 entropy bits per byte, 7.94505 minimum entropy bits per byte.
Price: US$50.
Acquisition: easy.
Performance: 400 Kbps claimed, 404 Kbps measured.
Robustness: high.
Integration: easy (USB).
Mechanism: semiconductor avalanche effect.
Openness: closed.
Source: http://ubld.it/products/truerng-hardware-random-number-generator/

OneRNG V3.0 External.
Vendor: Moonbase Otago (New Zealand).
Correctness: N/A (failed after sixty-nine days of testing).
Price: US$40.
Acquisition: medium (takes a while).
Performance: 350 Kbps claimed.
Robustness: N/A (failed after sixty-nine days of testing).
Integration: medium (USB but requires some initialization).
Mechanism: semiconductor avalanche effect and atmospheric noise.
Openness: open (both hardware and software).
Source: http://onerng.info

Chaos Key 1.0.
Vendor: Altus Metrum via Garbee and Garbee.
Correctness: 7.999956 entropy bits per byte, 7.94565 minimum entropy bits per byte.
Price: US$40.
Acquisition: easy.
Performance: 10Mbps claimed, 6.7Mbps measured (still remarkably fast).
Robustness: High.
Integration: easy (USB with device driver incorporated into kernel).
Mechanism: transistor noise.
Openness: open (both hardware and software).
Source: http://altusmetrum.org/ChaosKey/

Infinite Noise.
Vendor: Wayward Geek via Tindie.
Correctness: 7.999955 entropy bits per byte, 7.97759 minimum entropy bits per byte.
Price: US$35.
Acquisition: easy.
Performance: 259 Kbps claimed, 357 Kbps measured.
Robustness: high.
Integration: medium (requires building infnoise utility that must be run as root).
Mechanism: thermal noise.
Openness: open (both hardware and software).
Source: https://www.tindie.com/products/WaywardGeek/infinite-noise-true-random-number-generator/
Conclusions
If you're not concerned about openness, the US$99 TrueRNGpro delivers great performance at a reasonable price, is dirt simple to integrate into your Linux/GNU system, and is easy to acquire.
If you are concerned about openness, the US$50 FST-01 NeuG available from the Free Software Foundation is reasonably priced, fairly easy to acquire, and the FSF publishes its firmware source code and hardware schematics.
If you want to feel like you're living in a William Gibson novel, or have extraordinary requirements for an entropy mechanism beyond reproach, or need high performance, don't mind a bit of work to integrate it into your system, and have very deep pockets, the US$1100 Quantis is the way to go.
If you want something like the TrueRNGpro, but is maybe a little easier to carry in your laptop bag and use at the coffee shop, and can live with a little less performance, it's hard to beat the US$50 TrueRNG (the version 3 of which I'm still testing, but so far it looks great). You can one-click this from Amazon.com and have it day after tomorrow.
If you live in Australia or New Zealand, I couldn't blame you for checking out the devices designed by folks there. My luck with the OneRNG hasn't been good. But the BitBabbler White worked great, is IMNSHO worth every penny, and is a great open alternative to the FST-01 NeuG for anyone.
If you are using a platform that already incorporates a hardware entropy generator - as a component, a peripheral, or even a machine instruction - it may just be a matter of installing the rng-tools package and doing a bit of configuration. Or maybe just updating your kernel. Or it may be present in your system right now.
It's worth a look.
Repositories
The Scattergun repository, which includes the scattergun.sh test script and Makefile, software I wrote to use some of the generators, and the results of running the test script on each device, can be found on GitHub.
One never sets out on an epic quest without some traveling companions. There are a couple I can acknowledge. My office mate from my Bell Labs days, Doug Gibbons, was coincidentally working in this area and gave me much invaluable guidance. My occasional colleague Doug Young invited me to give a talk on this topic at Gogo Business Aviation, which incentivized me to firm up my thinking on this topic.
Update 2017-02-28
Apple, "iOS Security", Apple Inc., 2016-05
ArchWiki, "Random number generation", https://wiki.archlinux.org/index.php/Random_number_generation, 2017-09-02 (added 2018-01-02)
Atmel, "Trusted Platform Module LPC Interface", AT97SC3204, Atmel, 2013-03-20
Atmel, "Atmel Trusted Platform Module AT97SC3204/AT97SC3205 Security Policy", FIPS 140-2, level 1, version 4.3, Atmel, 2014-04-03
E. Barker, J. Kelsey, "Recommendation for Random Number Generation Using Deterministic Random Bit Generators", NIST Special Publication 800-90A, Revision 1, National Institute of Standards and Technology, 2015-06
E. Barker, J. Kelsey, "Recommendation for the Entropy Sources Used for Random Bit Generation", NIST Special Publication 800-90B, second draft, National Institute of Standards and Technology, 2016-01-27
R. Brown, D. Eddelbuettel, D. Bauer, "Dieharder: A Random Number Test Suite", version 3.31.1, http://www.phy.duke.edu/~rgb/General/dieharder.php, 2016-02-06
W. Gibson, Neuromancer, Ace, 1984
M. Green, "Attack of the week: 64-bit ciphers in TLS", https://blog.cryptographyengineering.com/2016/08/24/attack-of-week-64-bit-ciphers-in-tls/, 2016-08-24
M. Gulati, M. Smith, S. Yu, "Secure Enclave Processer for a System on a Chip", U. S. Patent 8,832,465 B2, Apple Inc., 2014-09-09
G. Heiser, K. Elphinstone, "L4 Microkernels: The Lessons from 20 Years of Research and Deployment", ACM Transactions on Computer Systems, 34.1, 2016-04
T. Hühn, "Myths about /dev/urandom", http://www.2uo.de/myths-about/urandom/, 2016-11-06
Intel, "Intel Digital Random Number Generator (DRNG) Software Implementation Guide", revision 2.0, Intel, 2014-05-15
Intel, "Intel Trusted Platform Module (TPM module-AXXTPME3) Hardware User's Guide", G21682-003, Intel
B. Koerner, "Russians Engineer a Brilliant Slot Machine Cheat - and Casinos Have No Fix", wired.com, 2014-06
E. Lim, sharing with me a personal communication he had with the developer of the BitBabbler, 2018-01-02
NIST, "Security Requirements for Cryptographic Modules", FIPS PUB 140-2, National Institute of Standards and Technology, 2001-05-25
NIST, "Minimum Security Requirements for Federal Information and Information Systems", FIPS PUB 200, National Institute of Standards and Technology, 2006-03
NIST, "Derived Test Requirements for FIPS PUB 140-2", National Institute of Standards and Technology, 2011-01-04
NIST, "Digital Signature Standard (DSS)", FIPS PUB 186-4, National Institute of Standards and Technology, 2013-07
NIST, "NIST Removes Cryptography Algorithm from Random Number Generator Recommendations", National Institute of Standards and Technology, 2014-04-21
NIST, "Implementation Guidance for FIPS PUB 140-2 and the Cryptographic Module Validation Program", National Institute of Standards and Technology, 2016-08-01
NIST, "SP800-90B Entropy Assessment", https://github.com/usnistgov/SP800-90B_EntropyAssessment, 2016-10-24
C. Overclock, "John Sloan and Hardware Entropy Generators", http://chipoverclock.com/2016/10/john-sloan-and-hardware-entropy.html, 2016-10-18
J. Schiller, S. Crocker, "Randomness Requirements for Security", RFC 4086, 2005-06
B. Schneier, "SHA1 Deprecation: What You Need to Know", Schneier on Security, https://www.schneier.com/blog/archives/2005/02/cryptanalysis_o.html, 2005-02-18
B. Schneier, "The Strange Story of Dual_EC_DRBG", Schneier on Security, https://www.schneier.com/blog/archives/2007/11/the_strange_sto.html, 2007-11
CWI, "SHAttered", http://shattered.it/, 2017-02-23
R. Snouffer, A. Lee, A. Oldehoeft, "A Comparison of the Security Requirements for Cryptographic Modules in FIPS 140-1 and FIPS 140-2", NIST Special Publication 800-29, National Institute of Standards and Technology, 2001-06
M. Stevens, E. Bursztein, P. Karpman, A. Albertini, Y. Markov, "The first collision for full SHA-1", CWI Amsterdam, Google Research, 2017-02-23
M. Stevens, E. Bursztein, P. Karpman, A. Albertini, Y. Markov, A. Petit Bianco, C. Baisse, "Announcing the first SHA1 collision", Google Security Blog, https://security.googleblog.com/2017/02/announcing-first-sha1-collision.html, 2017-02-23
TCG, "TCG Specification Architecture Overview", revision 1.4, Trusted Computing Group, 2007-08-02
TCG, "TCG PC Client Specific TPM Interface Specification (TIS)", version 1.2, revision 1.00, Trusted Computing Group, 2005-07-11
M. Turan, "IID Testing in SP 800 90B", Random Bit Generation Workship 2016, National Institute of Standards and Technology, 2016-05
J. Walker, "ENT: A Pseudorandom Number Sequence Test Program", https://www.fourmilab.ch/random/, 2016-02-27
Wikipedia, "Hardware random number generator", https://en.wikipedia.org/wiki/Hardware_random_number_generator, 2016-12-30
Wikipedia, "Comparison of hardware random number generators", https://en.wikipedia.org/wiki/Comparison_of_hardware_random_number_generators, 2017-02-19
Wikipedia, "Dual_EC_DRBG", https://en.wikipedia.org/wiki/Dual_EC_DRBG, 2017-01-02
Wikipedia, "Salsa20" (from which Chacha20 is derived), https://en.wikipedia.org/wiki/Salsa20, 2017-11-07
Wikipedia, "SHA-1", https://en.wikipedia.org/wiki/SHA-1, 2017-02-15
Wikipedia, "Trusted Platform Module", https://en.wikipedia.org/wiki/Trusted_Platform_Module, 2017-02-17
You could be forgiven if the thought occurred to you: hey, if we could just encrypt a message by multiplying it by a secret key (the message and the key being just numbers inside a computer), and decrypt the encrypted message by dividing it by that same secret key, the bad guys would find it almost impossible to brute force decrypt our encrypted message.
This is a issue even for very well funded government intelligence organizations. Thanks to Wikileaks and Edward Snowden, we now know that the U. S. National Security Agency (NSA) reads secrets by tapping into the unencrypted data stream, not by breaking the encryption, often with the cooperation of the service provider. (Updated 2017-03-10)
Similarly, while the NSA pursues mass surveillance, thanks to Wikileaks and an as of yet unknown source we now also know that the U. S. Central Intelligence Agency (CIA) pursues individual surveillance by hacking a mobile phone and accessing its data before it is encrypted (or after it is decrypted), not by breaking the encryption on the device. (Added 2017-03-10)With a large enough secret key, all the computing power in the world might not be enough to break our encryption. And as computers grow more powerful, if we get worried, we can just make our key a few bits longer, eat the (relatively) small increment in computing power necessary to encrypt (multiplying) and decrypt (dividing), and the computing power necessary for brute force cracking (factoring) of our encryption becomes so large that all the computing power in the universe wouldn't be enough.
And that's exactly what happens.
Almost all modern encryption algorithms are based on multiplication/factoring. But there are other trapdoor functions, and encryption algorithms based on them - elliptic curve cryptology is one you'll read about. Some Microsoft researchers discovered what is widely believed to be a backdoor deliberately engineered into one elliptic curve encryption algorithm - the Dual Elliptic Curve Deterministic Random Bit Generator or Dual_EC_DRBG - that was endorsed by the U.S. National Institute of Standards and Technology (NIST) as Federal Information Processing Standard (FIPS). Which is why studying this area is a bit like reading a spy thriller. Because it is a spy thriller.Why We Care
It is obvious now that the security of your encryption mechanism all revolves around keeping your secret key secret. If the bad guy has your secret key, you might as well be publishing your secret messages on Facebook.
You have to choose a secret key that the bad guy isn't likely to guess. Your birthday, or your mobile phone number, and what not, is a really bad idea.
And you have to have some secure way to communicate your secret key to the person who is to receive your encrypted messages. If the bad guy taps your communication channel and reads your secret key, he has the means to trivially break your encryption.
You also need a lot of secret keys. Every time you click on a web link whose Uniform Resource Locator (URL) uses the https protocol, like in https://www.google.com - the s standing for "secure" - you need a new secret key with which to encrypt the data going to the web server and coming back to your web browser.
So what your web browser does is it generates a new secret key for every such transaction, and it does so in a way that the bad guy is not likely to guess: it generates a random number to use as the key.
What I have described is symmetric key encryption - the key used for encryption is the same one used for decryption. Public key encryption - where the key used for encryption is different from the one used for decryption - is asymmetric. Public key encryption is beyond the scope of this article. (That's what guys like me say when they don't really understand something.) But public key encryption is so computationally expensive that it is typically used just for key exchange - securely transmitting the random number used for symmetric key encryption to the recipient of your message, after which the message or data stream is encrypted using the symmetric key mechanism I just described. Public key encryption solves the problem of how to transmit your secret symmetric key securely to your message recipient.The security of your encryption now all depends on the quality of your keys. The quality of your keys depends on the quality of your random numbers. And the quality - or unguessability - of your random numbers now depends on [1] the quality of the seed used to generate those random numbers (the more entropy the better), and [2] the period of the pseudo random number generator you are using (the longer the better).
And now we are on a mission to find a good seed.
The random Device Driver
If the option CONFIG_ARCH_RANDOM was enabled when the Linux kernel was configured and built, there is a device driver that generates random numbers. An application can acquire random numbers just by doing a read(2) against this driver. The driver exposes two interfaces in the /dev device directory: /dev/random and /dev/urandom. The random(4) manual page distinguishes between the two interfaces by telling us that /dev/random blocks (makes the application wait on the read) if the available entropy in the driver is exhausted, while /dev/urandom endlessly delivers as many values as the application cares to read. This raises the obvious question as to what exactly is /dev/urandom is returning if /dev/random is blocked because entropy is exhausted? And where does that entropy come from?

We can find the source code for this driver in drivers/char/random.c in the kernel source tree (3.10.105 is the version I perused). It's not that big. We'll start at the application interface and work backwards to discover where these random numbers from from.
/dev/urandom and /dev/random each have their own 512 bit pool that is used to store Cryptographically Secure Pseudo Random Numbers (CSPRNs). "Cryptographically Secure" means the random numbers are of high enough quality to be useful for cryptography, that is, for encryption. "Pseudo" is our first clue that they are the result of a pseudo-random number generator algorithm.
And indeed they are: they are generated by SHA-1, a well known cryptographic hash algorithm invented by the U. S. National Security Agency (NSA). SHA-1 takes an input - a seed - of any size and outputs a 160 bit number or cryptographic hash value. This hash value is said to be "cryptographic" because (you guessed it) it has properties useful for cryptography, one of the main ones being that given a SHA-1 hash value it is so expensive to try to brute force recover the original input value as to be computationally infeasible.
Whether this is true or not for SHA-1 today a matter of some debate in certain circles. Some flaws that have come to light in the SHA-1 design has shown that its effective internal state is not as large as once thought, reducing its period to within brute force attack range of at least state actors with sufficient computational resources. People who are deeply concerned about security no longer consider SHA-1 adequate. This means that the quality of the random bits produced by the random device driver in Linux depends even more now on the quality of the entropy sources feeding it.When an application reads from /dev/urandom or /dev/random, the driver removes bits from the appropriate pool, as long as there is entropy there to be had. The difference is when the driver determines that the level of entropy, as measured in bits, is insufficient, the driver blocks the application reading from /dev/random until the entropy is replenished. (We'll get to exactly what that means in a moment.) But when an application reads from /dev/urandom under the same circumstances, the driver cycles back through SHA-1, rehashing to generate a new output value. This can go on forever, as long as applications continue to read from /dev/urandom while there is insufficient entropy.
We have enough background now to know that the quality of the random numbers from this driver must depend on [1] the quality of the entropy being fed as a seed to SHA-1 for either /dev/random or /dev/urandom, and [2] the period of the SHA-1 algorithm when it gets used iteratively by /dev/urandom.
Note that there is still no source of entropy here. SHA-1 is a deterministic algorithm.
The SHA-1 function takes its input from a 4096 bit pool of entropy. The bits stored in this pool, no matter from whence they came, flow through a Cyclic Redundancy Check (CRC) polynomial that is used to merely mix bits from different entropy sources together, rendering the bits stored in the entropy pool anonymous, that is, unidentifiable as to their origin or meaning. This prevents a bad guy from learning anything useful about the internal state of the system from perusing the contents of this entropy pool.
Nope, still no source of entropy. The CRC is completely deterministic.
Updated 2018-01-02: The article "Random number generation" in the ArchWiki (also added to the references cited below) states that starting with version 4.8 of the Linux kernel, circa October 2016, the behavior of /dev/urandom has changed from what I describe here. I am just now starting to peruse the associated kernel source code. The article describes how the /dev/urandom driver is now seeded at start and then periodically reseeded with some true entropy, and subsequently generates new pseudo-random numbers using a Chacha20 cryptographic hash (replacing SHA-1). This is adequate for many applications, but as the article warns, not for long lived cryptographic keys. (Wikipedia also has an informative note on this in its article "/dev/random".)Measuring, and Consuming, Entropy
When the driver blocks a read on /dev/random, it is not measuring entropy based on the number of bits in either the 512 bit CSPRN pool used by /dev/random, nor on the number of bits in the 4096 bit entropy pool that feeds the SHA-1 algorithm. They are not that kind of First In First Out (FIFO) pools. Instead the driver tries to measure the effective randomness of the bits flowing into the CRC. It does this by measuring the first and second derivatives of the values for each of the entropy sources feeding the CRC.
This sounds a lot more high falutin' than it is. The driver merely looks to see if the difference between successive values of the original entropy data is changing (the first derivative), and if the difference between successive values of the first derivative is changing (the second derivative). From these values that are the result of simple subtractions, it computes an approximate measure of the entropy, or amount of randomness, in the data feeding the entropy pool. It is when this measure reaches zero that the behavior of both /dev/random and /dev/urandom changes.
You can read this measure of entropy but just looking at the value of the /proc file system entry /proc/sys/kernel/random/entropy_avail. You can do this from the command line by just using the cat command. But if you do so, you'll notice something interesting: every time you run the command, the amount of entropy is reduced!
This is because the kernel itself is a consumer of entropy, even if the entropy is not being used to generate encryption keys. The Linux kernel implements a feature called Address Space Layout Randomization (ASLR). Whenever the kernel dynamically allocates memory, including to run processes like the cat command, it reads bits from /dev/urandom to use to randomize where in the virtual memory address space the allocated memory block is placed.
This makes it much more difficult for the bad guy to attack the kernel by, for example, using kernel exploits - also known as bugs - to deliberately fool the kernel into overflowing buffers, resulting in overwriting other kernel data structures or even executable instructions.
As result, the pool of available entropy in the kernel driver is continuously being consumed.
Remarkably, some researchers have recently found a way to defeat ASLR, or at least reduce its effectiveness, by examining values stored in the cache and virtual memory management hardware of the microprocessor.Sources of Entropy, and Lack of Them
So exactly where is the entropy in the kernel random driver coming from? As I mentioned before, digital computer systems kinda suck by design at non-determinacy. So entropy in Linux comes from natural sources of non-determinism: measured latencies of physical I/O devices like spinning disks; activity by users of human interface devices (HID) like keyboards and mice; inter arrival time of network packets and interrupts; variation in the firing of timers; and other sources of unpredictable behavior.
The random driver contains a kernel API by which other device drivers in the system can report these values and add them to the entropy pool. You can find calls to this API littered throughout the Linux kernel. Here are some to look for, using your favorite source code browser.
add_disk_randomness
add_device_randomness
add_timer_randomness
add_input_randomness
add_interrupt_randomness
add_hwgenerator_randomnessIt was at this point in my fiddling with GnuPG, way back in 2007, that I began to get concerned. I was working on an embedded Linux product that ran completely from RAM disk. It had no interactive users. It only rarely used the network. Most of the time it spent dealing with an FPGA whose activity was based on a highly precise clock synchronized to GPS time using a phase locked loop.
I came to realize that there was almost no non-determinacy in the system. My product spent most of its time with little or no entropy. Which meant that /dev/random was effectively unusable, and the quality of the random numbers from /dev/urandom kinda sucked.
I realized that this could be a issue with all embedded Linux systems. Over time, I was to discover that this situation was hardly unique to me, or even to embedded systems.
Virtual machines running Linux - the backbone of cloud based computing - frequently ran short of usable entropy, because their I/O devices were for the most part nothing more than software abstractions on top of the system on which they ran, and which exhibited little or no random behavior.
And even an honest to goodness actual Linux server may have little or no entropy available when it first boots up, which is exactly when it may be establishing secure socket layer (SSL) connections to other servers, long lived connections that were made using poor quality seeds to their encryption algorithms.
What we needed was a reliable source of true entropy that could be easily integrated into products built around the Linux/GNU stack, a source that would not rely on largely hypothetical non-determinancy.
Note that the implementation of /dev/random and /dev/urandom are virtually identical. Both deliver random bits from the same entropy pool, filled from the same entropy sources, mixed with the same CRC polynomial, and conditioned by the same SHA-1 algorithm. The only difference is what they do when the estimated entropy in the driver is exhausted. So the answer to my original question back in 2007 about whether to use /dev/random or /dev/urandom is:
- always use /dev/urandom,
- but make sure there is a high quality source of entropy in the system,
- and use /dev/urandom to frequently reseed a pseudo random number generator to avoid detectable repeating patterns.
The issue about reseeding a PRNG before it repeats is not an idle concern. Security folks are starting to become worried about long lived Transport Layer Security (TLS) sessions, TLS being an encryption mechanism used for Internet traffic. It has been demonstrated that the TLS encryption can be brute force cracked if enough blocks from the encrypted TLS stream are collected. "Enough" is a big number - billions - but it is within the realm of practicality for adversaries with sufficient resources.Entropy is a Natural Resource
There are a number of physical processes that exhibit behavior that is effectively unpredictable and which can be digitized. These sources of entropy can be broadly divided into two categories: quantum or classical.
Quantum entropy sources are, as far as we know today, wired right into the physical nature of reality. Our current understanding of physics leads us to believe that there is no way to externally influence such entropy sources. Examples of quantum entropy include whether a photon passes through or is reflected by a partially silvered mirror; when a radioactive particle decays; when an electron tunnels through the band gap of a transistor to its base; when a photon falls on a photodiode and creates an electrical current.
Classic entropy sources may be said to be more chaotic than random, that is, influenced by environmental factors that are typically beyond our control. Examples of classic entropy include thermal noise from a resistor; electronic noise from an avalanche diode or from a zener diode in breakdown; atmospheric noise from a radio receiver; analog/digital convertor noise. These are all noise sources that a competent electrical engineer would normally work hard to eliminate in any design.
Each of these entropy sources can be amplified, instrumented, and digitized to produce a string of ones and zeros. However, even though they are unpredictable processes, such processes may not be unbiased: they may be more likely to produce ones or zeros. The bias can occur from practically unmeasureable variations in materials, or from minuscule differences in the sampling rate of the digitization, so that even in a modern semiconductor fabrication process, successive devices may yield very slightly different results.
A simple algorithm for whitening the bit stream - turning it into true white noise where ones and zeros occur with equal probability - is a problem solved long ago by none other than mathematician, computer scientist, information theorist, and Cold War strategist John von Neumann.
Every hardware entropy generator consists of (at least) three stages: a hardware process that generates true entropy, a stage that digitizes the entropy into a stream of ones and zeros, and a whitening stage that conditions the binary stream into white noise. These stages are typically implemented in hardware, or microcontroller firmware, embedded inside the hardware entropy generator.
Testing Entropy in the Short Run
For hardware entropy generators destined for use in applications which must conform to U.S. Federal Information Processing Standards (FIPS), which include not just U.S. government systems, or systems used by U.S. government contractors, but also commercial companies or regional agencies who just think such conformance is a good idea (or, as it turns out, manufacturers of electronic games of chance destined for gambling casinos that don't want to be ripped off), the U. S. National Institute of Standards and Technology (NIST) defines a set of statistical tests, FIPS 140-2, to be continuously run on the output of such generators to insure that they remain unbiased and have not failed in some non-obvious way. This is a fourth stage of such generators.
Some of the generators I have tested implement these FIPS tests themselves, but most take advantage of the rngd(8) user space daemon that is part of the rng-tools package available for most Linux/GNU distributions. rngd implements these tests in software against any hardware entropy generator for which it is configured to extract entropy to be injected via ioctl into the random device driver.
For most of the hardware entropy generators that I have tested, it is a very simple matter to integrate them into the system using rngd: usually a matter of installing the rng-tools package, doing some minor editing to the configuration file /etc/default/rng-tools, and sometimes a little udev rule hacking so that the generator shows up as a serial device in /dev.
Verifying Entropy in the Long Run
In addition to the FIPS tests, which are fast enough to be done in real-time, several folks who are interested in such things have developed suites of tests to be run against hardware entropy generators, and pseudo random number generators in general, to verify their broad long-term statistical properties. Each of these tests or suites of tests consume anywhere from kilobytes to terabytes of random bits, and require anywhere from seconds to weeks to run, even on a fast processor with a high-speed interface to the generator.
Scattergun is the code-name for my project to test consumer-grade hardware entropy generators and some software pseudo random number generators. It consists of the test script scattergun.sh, a Makefile to drive it, and a smattering of supporting software required to use the dozen or so generators that I own. (The supporting software included in Scattergun might be really useful to anyone using the more exotic generators, independent of the test script.) Scattergun is open source and can be found on GitHub. The raw results of all the testing are part of that repository as well. A link to the repository can be found near the end of this article.
Here is a brief description of the tests that the Scattergun script runs. The Scattergun script runs all of them, serially, accessing the hardware random number generator directly, without requiring that the generator be integrated into the system.
rngtest. Like rngd, rngtest is installed as part of the rng-tools package. It splits out the FIPS 140-2 tests that rngd runs in real-time into a command line tool where they can be run on demand. If a generator can't pass rngtest, it's not going to integrate into the system using rngd.
bitmap. This clever test ("clever" because I didn't think of it) exploits the ability of the human eyes and brain to perceive patterns in complex data. It extracts sufficient bits from a hardware entropy generator to create a 256 x 256 pixel Portable Network Graphics (PNG) file in 8-bit color. A successful generator should produce a PNG file that, in the words of one of my favorite authors William Gibson, "is the color of television, tuned to a dead channel". It is interesting to compare PNG files from various entropy sources and realize you can detect that the source only produces, for example, positive numbers because the most significant bit in each number being zero creates a distinct pattern, or it limits the dynamic range of values in some way that creates higher contrast colors.

This bitmap is from the hardware random number generator built into the Broadcom chip used on the Raspberry Pi 3.

This bitmap is from the random(3) C function that produces positive long integers.

This bitmap is from the mrand48(3) C function that produces positive and negative long integers.
ent. This is a quick "pseudorandom number sequence test program" written by John Walker. Some Linux/GNU distributions provide ent as an installable package. For those that don't, it can be easily downloaded from his web site, built, and installed. I like ent because it quickly provides an estimate of the effective entropy per byte, e.g. 7.999958 bits.
SP800-90B. This is a large suite of tests written in Python, developed by NIST, and made available on GitHub. It takes one or more hours to run on the typical generator. During this long duration side project, the repo on GitHub has been occasionally updated, so the SP800-90B tests have evolved as I've been using it. Since this suite is a NIST standard, its results probably carry more weight in certain circles.
dieharder. This is an enormous suite of tests developed by Robert Brown, a physicist at Duke University. Its name was inspired by the earlier diehard suite of statistical tests developed by George Marsaglia (and of course the Bruce Willis movie franchise). This dieharder suite consumes about a terabyte of entropy and can run for days or even weeks, depending on the speed of the hardware entropy generator, the interface to it, and the processor on which the test is running. It even drove one of the generators (OneRNG) I tested into failure due to overheating. I like that about it.
If you examine the results of these tests in the Scattergun GitHub repo, you will notice that some of the tests identify the generator as "weak", and some tests may even fail. This is not unusual. Statistically speaking, a sequence of numbers that doesn't look random is just as likely to be generated as any other sequence, so an occasional poor result is to be expected. It is when a lot of tests fail that you need to be concerned.
Shapes and Sizes (added 2017-03-03)
Hardware devices that generate true entropy, no matter what physical process they use to do so, come in a lot of shapes and sizes, with a variety of interfaces and features. Most of these can be integrated into your Linux/GNU system using the rngd(8) user space daemon from the rng-tools package. Some are already built right into the random(4) driver and just require the correct kernel configuration option (which may already be there).
External devices. Most of the generators I tested are external devices that connect to the host computer via the Universal Serial Bus (USB). Even so, there was a wide variety of software interfaces to these devices. The easiest enumerate as a serial port, typically requiring some minor udev rule hacking, and were trivial to use by just reading random bits from the port (TrueRNG2, TrueRNG3, TrueRNGpro, FST-01/NeuG). Some enumerated as a serial port, but required software to write commands to that port to initialize the device (OneRNGs). Some USB generators required a vendor-provided user-space utility to read from them (BitBabblers). One required a substantial software development effort (that I've done for you, yay!) using a vendor-provided library (Quantis).
Internal devices. The OneRNG comes in a form factor made to attach to an internal USB connector now present (as I was to learn) on many motherboards.
Internal cards. I didn't test it, but the the Quantis is available in a version with multiple entropy sources on a PCI-bus card.
Motherboard components. Although I didn't test it, Apple iPhones that use the A7 processor (the iPhone 5S and later) have a co-processor called the Secure Enclave Processor (SEP). The SEP has its own ARM core and has as a peripheral a hardware entropy generator. This generator is used to seed the encryption used by the iPhone.
Many personal computers intended for the enterprise or government markets include a Trusted Platform Module (TPM). The TPM, an industry standard created by the Trusted Computing Group (TCG), and examples of which are manufactured by several vendors, is similar in function to the SEP, and includes a hardware entropy generator. Even if you don't use the other features of the TPM, you can easily incorporate the TPM's generator into your Linux/GNU system as an entropy source. I've tested TPMs from two different vendors, in a laptop and in a server, belonging to one of my clients. Because that work was covered under non-disclosure, I don't include those results here. But you may have a TPM with a hardware entropy generator on your system already.
(Updated 2017-07-20) I now have a server that incorporates a TPM chip and I've added a test of its hardware entropy generator.
System peripherals. Some System on a Chips (SoC) feature entropy generators as a built-in peripheral. The Broadcom SoC used by the Raspberry Pi 2 and 3 boards (I haven't tested the Raspberry Pi 1) have such a peripheral. It's not enabled by default, but it's easy to do so by just loading the appropriate device driver module and using rngd(8).
Machine instructions. Recent Intel processors have implemented a hardware entropy source, and a PRNG that is automatically periodically reseeded by that source, as machine instructions: rdseed (Broadwell family) and rdrand (Ivy Bridge family) respectively. Latest versions of the Linux kernel destined for these processors automatically make use of rdrand to augment the legacy entropy sources in the random device driver.
There is some controversy about these instructions thanks to Intel's collaboration in the past with the U. S. National Security Agency and the closed nature of their implementation. The Linux kernel maintainers have said that this is why they don't use rdrand as their sole entropy source. However, by this time you will be concerned that it may effectively be the only entropy source on an embedded system using an Intel processor. This may be justification enough to use an additional entropy source. One of my clients took the wise precaution on an Intel-based embedded product of also using the entropy generator on the non-Intel TPM chip that was available on the ComExpress module they used in their design.Aspects (updated 2017-04-23)
Remarkably, there are a lot of hardware entropy generators on the market. Making an informed decision as to which one you want to use requires that you consider what your priorities are. It is a surprisingly multi-dimensional decision matrix.
Correctness. This is the easy one. I'll just jump right to the punch line and tell you that all of the hardware entropy generators that completed the Scattergun script did fine. One device failed during testing, and a new version (said to be more tolerant of heating) will start testing soon. Another is being tested now, and looks good. I noted the number of entropy bits (relative to eight bits) reported by ent, and the minimum entropy (ditto) reported by SP800-90B for its Independent and Identically Distributed (IID) test.
Price. For hardware entropy generators, I've paid as little as US$50 and as much as US$1100 (definitely an outlier on the price axis). There is no correctness difference, and not as much performance difference as you might expect, between the far ends of that range. You may be able to purchase a perfectly adequate hardware entropy generator for, if not lunch money, at least good dinner money, depending on what your other priorities are.
Acquisition. One of my generators I purchased by clicking the one-click ordering button on Amazon.com, had US$50 or so deducted off my credit card, and thanks to Amazon Prime had the device delivered to my front door in a couple of days. For others, I had to exchange encrypted email, send FAXes to Australia, and then wait for a shipment from China. All of the other devices fall somewhere on that range of effort to acquire.
Performance. The performance measurements should probably be taken with at least a small grain of salt, since there were a number of buffers between the actual device and the test suite. Even so, there is probably some merit in comparing the numbers. There was a fair amount of performance difference, in terms of entropy bits per second, among the generators. Some of the generators are peripherals built into an SoC (Raspberry Pi 2 and 3). Some are machine instructions built directly into the processor (rdrand and rdseed). Most are external USB devices. There was little correlation between the price of the device and its performance. But the interface typically made a difference. As you would expect, generally the internal devices performed better. But the best performer was an US$40 device with a USB interface (Chaos Key); the second best was the US$1100 device that also interfaced by USB (Quantis); the third place performer was a US$99 USB device (TrueRNGpro).
Robustness. One of the devices (OneRNG) failed during testing, probably due to overheating, which was a common complaint by users of this device. The vendor is now shipping a new version that I have received but have not tested yet. None of the other devices failed during testing, although I did manage to destroy one (OneRNG) designed for an internal USB connection on a motherboard, by hooking it up incorrectly.
Integration. Some of these devices were trivial to integrate into the system, requiring at most just a little udev hacking to get their USB interface recognized as a serial device. Some required use of a vendor-supplied user-space daemon or script (OneRNG, BitBabbler). And some (Quantis) required a substantial effort in software development using a vendor-supplied library; it's performance might be worth it.
Openness. This is one domain where it may pay to be a foil-hat-wearing member of the conspiracy theory club. Some of the devices were completely open, their firmware source code and hardware schematics published by the vendor. Most were completely closed and proprietary. Some of them (TrueRNG2, TrueRNG3, TrueRNGpro) were designed by folks within commuting distance of the headquarters of the National Security Agency; this is probably not a coincidence: that neck of the woods would tend to attract engineers who know how to design stuff like this. You'll have to decide how paranoid you are about these kinds of things.
Hardware Entropy Generators I Have Known (updated 2017-04-23)
Here is a rundown of the hardware entropy generators that I own, listed in the order that I tested them. Or am testing them. Or will be testing them.
Unfortunately, the Scattergun script doesn't lend itself to precise performance measurements since the script is fed data from the device through a UNIX pipe. Never the less, I did note the speed at which random bits were consumed from the pipe, figuring that over large amounts of data it would even out to more or less match the rate at which data was introduced into the pipe. All speeds are in kilobits or megabits per second.

TrueRNGpro (right).
Vendor: ublt.it (U.S.).
Correctness: 7.999958 entropy bits per byte, 7.94464 minimum entropy bits per byte.
Price: US$99.
Acquisition: easy.
Performance: 3.2Mbps claimed, 3.4Mbps measured.
Robustness: high.
Integration: easy (USB) (and the LEDs are comforting too).
Mechanism: semiconductor avalanche effect (two parallel sources).
Openness: closed.
Source: http://ubld.it/products/truerngpro

Vendor: ID Quantique (Switzerland).
Correctness: 7.999962 entropy bits per byte, 7.94601 minimum entropy bits per byte.
Price: US$1100 (E990).
Acquisition: medium.
Performance: 4Mbps claimed, 3.9Mbps measured.
Robustness: high.
Integration: difficult (USB but requires software development using vendor library).
Mechanism: beam splitter with photon counter (quantum effect).
Openness: closed.
Source: http://www.idquantique.com/random-number-generation/quantis-random-number-generator/

Vendor: Broadcom (BCM2836 SoC).
Correctness: 7.999954 entropy bits per byte, 7.94918 minimum entropy bits per byte.
Price: US$35 (Raspberry Pi 2).
Acquisition: easy.
Performance: 824Kbps measured.
Robustness: high.
Integration: easy (device driver).
Mechanism: undocumented.
Openness: open software, closed hardware.
Source: https://www.raspberrypi.org/products/raspberry-pi-2-model-b/

FST-01 NeuG.
Vendor: Flying Stone Technology via GNU Press (Free Software Foundation).
Correctness: 7.999959 entropy bits per byte, 7.94114 minimum entropy bits per byte.
Price: US$50.
Acquisition: easy.
Performance: 602 Kbps claimed, 653 Kbps measured.
Robustness: high.
Integration: easy (USB).
Mechanism: analog/digital convertor noise.
Openness: open (both software and hardware).
Source: https://shop.fsf.org/storage-devices/neug-usb-true-random-number-generator

Vendor: Intel (i7-6700T in my test).
Correctness: 7.999957 entropy bits per byte, 7.94404 minimum entropy bits per byte.
Price: N/A.
Acquisition: N/A.
Performance: 1600Mbps claimed, 228Mbps measured.
Robustness: high.
Integration: easy (integrated into random device driver in later Linux kernels).
Mechanism: AES PRNG periodically reseeded by the rdseed mechanism (see below).
Openness: open software, closed hardware.
Source: https://software.intel.com/en-us/articles/intel-digital-random-number-generator-drng-software-implementation-guide
rdseed (machine instruction in the Broadwell processor family and later).
Vendor: Intel (i7-6700T in my test).
Correctness: 7.999958 entropy bits per byte, 7.9408 minimum entropy bits per byte.
Price: N/A.
Acquisition: N/A.
Performance: 3.5 Mbps measured.
Robustness: high.
Integration: easy (integrated into random device driver in later Linux kernels).
Mechanism: thermal noise.
Openness: open software, closed hardware.
Source: https://software.intel.com/en-us/articles/intel-digital-random-number-generator-drng-software-implementation-guide
WEC TPM TCG 1.2 FW 5.81
Vendor: Winbond Electronics Corporation.
Correctness: TBD.
Price: N/A (embedded inside a Dell OptiPlex 7040 Micro Form Factor BTX desktop PC).
Acquisition: N/A.
Performance: TBD but not good. As of 2018-08-10 I've been running the Scattergun test suite against this Trusted Platform Module, embedded as a feature inside one of my otherwise unused Linux servers, for over a year. And while it continues to make progress, albeit very slowly, I don't have a projection of when it will finish. Clearly something is seriously amiss, since it made progress more quickly at the beginning. I'm limited as to the diagnostics I can run without interfering, or worse inadvertently interrupting, the test. But I don't see any errors in the log, as the suite continues to extract entropy from the /dev/hwrng device that exposes the TPM's entropy generator. I'll have to start looking much more closely at the tpm-rng kernel model to see how it's implemented. Update 2022-02-03: After four years and five months of running Scattergun against this device, my lab lost power - due to the same high winds that propagated the tragic Marshall fire across Boulder County on 2021-12-28 - long enough that the UPS powering this system finally ran dry. At the moment it failed, it was near the end of the last test suite in the Scattergun meta-suite. But saying it was "near the end" really means nothing. It continued to make slow progress, but could have run for several more years. Again, I'm assuming there was a problem somewhere in the test setup.
Robustness: TBD.
Integration: easy (loading tpm-rng kernel module exposes /dev/hwrng).
Mechanism: N/A.
Openness: open software, apparently closed firmware and hardware.
Source: N/A.

Raspberry Pi 3 (64-bit) BCM2708 HWRNG.
Vendor: Broadcom (BCM2837 SoC).
Correctness: 7.999956 entropy bits per byte, 7.9334 minimum entropy bits per byte.
Price: US$35 (Raspberry Pi 3).
Acquisition: easy.
Performance: 1Mbps measured.
Robustness: high.
Integration: easy (device driver).
Mechanism: undocumented.
Openness: open software, closed hardware.
Source: https://www.raspberrypi.org/products/raspberry-pi-3-model-b/

Vendor: ublt.it (U.S.).
Correctness: 7.999958 entropy bits per byte, 7.94464 minimum entropy bits per byte.
Price: US$50.
Acquisition: easy.
Performance: 350 Kbps claimed, 367 Kbps measured.
Robustness: high.
Integration: easy (USB).
Mechanism: semiconductor avalanche effect.
Openness: closed.
Source: http://ubld.it/products/truerng-hardware-random-number-generator/

Vendor: Moonbase Otago (New Zealand).
Correctness: N/A.
Price: US$40.
Acquisition: medium (takes a while).
Performance: 350 Kbps claimed.
Robustness: failed during testing (overheating a common complaint, may be fixed in V3.0).
Integration: medium (USB but requires some initialization).
Mechanism: semiconductor avalanche effect and atmospheric noise.
Openness: open (both hardware and software).
Source: http://onerng.info

OneRNG v2.0 Internal.
Vendor: Moonbase Otago (New Zealand).
Correctness: N/A.
Price: US$40.
Acquisition: medium (takes a while).
Performance: 350 Kbps claimed.
Robustness: I managed to fry my one unit by hooking the internal USB cable up incorrectly.
Integration: medium (internal USB but requires some initialization).
Mechanism: semiconductor avalanche effect and atmospheric noise.
Openness: open (both hardware and software).
Source: http://onerng.info

Vendor: VoiceTronix Pty. Ltd. (Australia).
Correctness: 7.999951 entropy bits per byte, 7.94498 minimum entropy bits per byte.
Price: AUS$199.
Acquisition: difficult (required a fair amount of effort).
Performance: 2.5 Mbps claimed, 1.2 Mbps measured.
Robustness: high.
Integration: medium (USB but requires vendor supplied user-space daemon).
Mechanism: shot noise, Johnson-Nyquist noise, flicker noise, RF noise (multiple sources).
Openness: open software and hardware.
Source: http://bitbabbler.org
BitBabbler Black (top).
Vendor: VoiceTronix Pty. Ltd. (Australia).
Correctness: 7.999963 entropy bits per byte, 7.93873 minimum entropy bits per byte.
Price: AUS$49.
Acquisition: difficult (required a fair amount of effort).
Performance: 625 Kbps claimed, 307 Kbps measured.
Robustness: high.
Integration: medium (USB but requires vendor supplied user-space daemon).
Mechanism: shot noise, Johnson-Nyquist noise, flicker noise, RF noise.
Openness: open software and hardware.
Source: http://bitbabbler.org

Vendor: ublt.it (U.S.).
Correctness: 7.999956 entropy bits per byte, 7.94505 minimum entropy bits per byte.
Price: US$50.
Acquisition: easy.
Performance: 400 Kbps claimed, 404 Kbps measured.
Robustness: high.
Integration: easy (USB).
Mechanism: semiconductor avalanche effect.
Openness: closed.
Source: http://ubld.it/products/truerng-hardware-random-number-generator/

Vendor: Moonbase Otago (New Zealand).
Correctness: N/A (failed after sixty-nine days of testing).
Price: US$40.
Acquisition: medium (takes a while).
Performance: 350 Kbps claimed.
Robustness: N/A (failed after sixty-nine days of testing).
Integration: medium (USB but requires some initialization).
Mechanism: semiconductor avalanche effect and atmospheric noise.
Openness: open (both hardware and software).
Source: http://onerng.info

Chaos Key 1.0.
Vendor: Altus Metrum via Garbee and Garbee.
Correctness: 7.999956 entropy bits per byte, 7.94565 minimum entropy bits per byte.
Price: US$40.
Acquisition: easy.
Performance: 10Mbps claimed, 6.7Mbps measured (still remarkably fast).
Robustness: High.
Integration: easy (USB with device driver incorporated into kernel).
Mechanism: transistor noise.
Openness: open (both hardware and software).
Source: http://altusmetrum.org/ChaosKey/

Infinite Noise.
Vendor: Wayward Geek via Tindie.
Correctness: 7.999955 entropy bits per byte, 7.97759 minimum entropy bits per byte.
Price: US$35.
Acquisition: easy.
Performance: 259 Kbps claimed, 357 Kbps measured.
Robustness: high.
Integration: medium (requires building infnoise utility that must be run as root).
Mechanism: thermal noise.
Openness: open (both hardware and software).
Source: https://www.tindie.com/products/WaywardGeek/infinite-noise-true-random-number-generator/
Conclusions
If you're not concerned about openness, the US$99 TrueRNGpro delivers great performance at a reasonable price, is dirt simple to integrate into your Linux/GNU system, and is easy to acquire.
If you are concerned about openness, the US$50 FST-01 NeuG available from the Free Software Foundation is reasonably priced, fairly easy to acquire, and the FSF publishes its firmware source code and hardware schematics.
If you want to feel like you're living in a William Gibson novel, or have extraordinary requirements for an entropy mechanism beyond reproach, or need high performance, don't mind a bit of work to integrate it into your system, and have very deep pockets, the US$1100 Quantis is the way to go.
If you want something like the TrueRNGpro, but is maybe a little easier to carry in your laptop bag and use at the coffee shop, and can live with a little less performance, it's hard to beat the US$50 TrueRNG (the version 3 of which I'm still testing, but so far it looks great). You can one-click this from Amazon.com and have it day after tomorrow.
If you live in Australia or New Zealand, I couldn't blame you for checking out the devices designed by folks there. My luck with the OneRNG hasn't been good. But the BitBabbler White worked great, is IMNSHO worth every penny, and is a great open alternative to the FST-01 NeuG for anyone.
If you are using a platform that already incorporates a hardware entropy generator - as a component, a peripheral, or even a machine instruction - it may just be a matter of installing the rng-tools package and doing a bit of configuration. Or maybe just updating your kernel. Or it may be present in your system right now.
It's worth a look.
Repositories
The Scattergun repository, which includes the scattergun.sh test script and Makefile, software I wrote to use some of the generators, and the results of running the test script on each device, can be found on GitHub.
https://github.com/coverclock/com-diag-scattergunThe photographs, diagrams, and PNG images that are results of testing can be found on Flickr.
https://www.flickr.com/photos/johnlsloan/albums/72157660632647214Acknowledgements
One never sets out on an epic quest without some traveling companions. There are a couple I can acknowledge. My office mate from my Bell Labs days, Doug Gibbons, was coincidentally working in this area and gave me much invaluable guidance. My occasional colleague Doug Young invited me to give a talk on this topic at Gogo Business Aviation, which incentivized me to firm up my thinking on this topic.
Update 2017-02-28
Cryptographic hash functions like SHA-1 are a cryptographer’s swiss army knife. You’ll find that hashes play a role in browser security, managing code repositories, or even just detecting duplicate files in storage. Hash functions compress large amounts of data into a small message digest. As a cryptographic requirement for wide-spread use, finding two messages that lead to the same digest should be computationally infeasible. Over time however, this requirement can fail due to attacks on the mathematical underpinnings of hash functions or to increases in computational power.
Today, more than 20 years after of SHA-1 was first introduced, we are announcing the first practical technique for generating a collision.
-- M. Stevens et al., "Announcing the first SHA1 collision", Google Security Blog, 2017-02-23Sources
Apple, "iOS Security", Apple Inc., 2016-05
ArchWiki, "Random number generation", https://wiki.archlinux.org/index.php/Random_number_generation, 2017-09-02 (added 2018-01-02)
Atmel, "Trusted Platform Module LPC Interface", AT97SC3204, Atmel, 2013-03-20
Atmel, "Atmel Trusted Platform Module AT97SC3204/AT97SC3205 Security Policy", FIPS 140-2, level 1, version 4.3, Atmel, 2014-04-03
E. Barker, J. Kelsey, "Recommendation for Random Number Generation Using Deterministic Random Bit Generators", NIST Special Publication 800-90A, Revision 1, National Institute of Standards and Technology, 2015-06
E. Barker, J. Kelsey, "Recommendation for the Entropy Sources Used for Random Bit Generation", NIST Special Publication 800-90B, second draft, National Institute of Standards and Technology, 2016-01-27
R. Brown, D. Eddelbuettel, D. Bauer, "Dieharder: A Random Number Test Suite", version 3.31.1, http://www.phy.duke.edu/~rgb/General/dieharder.php, 2016-02-06
W. Gibson, Neuromancer, Ace, 1984
M. Green, "Attack of the week: 64-bit ciphers in TLS", https://blog.cryptographyengineering.com/2016/08/24/attack-of-week-64-bit-ciphers-in-tls/, 2016-08-24
M. Gulati, M. Smith, S. Yu, "Secure Enclave Processer for a System on a Chip", U. S. Patent 8,832,465 B2, Apple Inc., 2014-09-09
G. Heiser, K. Elphinstone, "L4 Microkernels: The Lessons from 20 Years of Research and Deployment", ACM Transactions on Computer Systems, 34.1, 2016-04
T. Hühn, "Myths about /dev/urandom", http://www.2uo.de/myths-about/urandom/, 2016-11-06
Intel, "Intel Digital Random Number Generator (DRNG) Software Implementation Guide", revision 2.0, Intel, 2014-05-15
Intel, "Intel Trusted Platform Module (TPM module-AXXTPME3) Hardware User's Guide", G21682-003, Intel
B. Koerner, "Russians Engineer a Brilliant Slot Machine Cheat - and Casinos Have No Fix", wired.com, 2014-06
E. Lim, sharing with me a personal communication he had with the developer of the BitBabbler, 2018-01-02
NIST, "Security Requirements for Cryptographic Modules", FIPS PUB 140-2, National Institute of Standards and Technology, 2001-05-25
NIST, "Minimum Security Requirements for Federal Information and Information Systems", FIPS PUB 200, National Institute of Standards and Technology, 2006-03
NIST, "Derived Test Requirements for FIPS PUB 140-2", National Institute of Standards and Technology, 2011-01-04
NIST, "Digital Signature Standard (DSS)", FIPS PUB 186-4, National Institute of Standards and Technology, 2013-07
NIST, "NIST Removes Cryptography Algorithm from Random Number Generator Recommendations", National Institute of Standards and Technology, 2014-04-21
NIST, "Implementation Guidance for FIPS PUB 140-2 and the Cryptographic Module Validation Program", National Institute of Standards and Technology, 2016-08-01
NIST, "SP800-90B Entropy Assessment", https://github.com/usnistgov/SP800-90B_EntropyAssessment, 2016-10-24
C. Overclock, "John Sloan and Hardware Entropy Generators", http://chipoverclock.com/2016/10/john-sloan-and-hardware-entropy.html, 2016-10-18
J. Schiller, S. Crocker, "Randomness Requirements for Security", RFC 4086, 2005-06
B. Schneier, "SHA1 Deprecation: What You Need to Know", Schneier on Security, https://www.schneier.com/blog/archives/2005/02/cryptanalysis_o.html, 2005-02-18
B. Schneier, "The Strange Story of Dual_EC_DRBG", Schneier on Security, https://www.schneier.com/blog/archives/2007/11/the_strange_sto.html, 2007-11
CWI, "SHAttered", http://shattered.it/, 2017-02-23
R. Snouffer, A. Lee, A. Oldehoeft, "A Comparison of the Security Requirements for Cryptographic Modules in FIPS 140-1 and FIPS 140-2", NIST Special Publication 800-29, National Institute of Standards and Technology, 2001-06
M. Stevens, E. Bursztein, P. Karpman, A. Albertini, Y. Markov, "The first collision for full SHA-1", CWI Amsterdam, Google Research, 2017-02-23
M. Stevens, E. Bursztein, P. Karpman, A. Albertini, Y. Markov, A. Petit Bianco, C. Baisse, "Announcing the first SHA1 collision", Google Security Blog, https://security.googleblog.com/2017/02/announcing-first-sha1-collision.html, 2017-02-23
TCG, "TCG Specification Architecture Overview", revision 1.4, Trusted Computing Group, 2007-08-02
TCG, "TCG PC Client Specific TPM Interface Specification (TIS)", version 1.2, revision 1.00, Trusted Computing Group, 2005-07-11
M. Turan, "IID Testing in SP 800 90B", Random Bit Generation Workship 2016, National Institute of Standards and Technology, 2016-05
J. Walker, "ENT: A Pseudorandom Number Sequence Test Program", https://www.fourmilab.ch/random/, 2016-02-27
Wikipedia, "Hardware random number generator", https://en.wikipedia.org/wiki/Hardware_random_number_generator, 2016-12-30
Wikipedia, "Comparison of hardware random number generators", https://en.wikipedia.org/wiki/Comparison_of_hardware_random_number_generators, 2017-02-19
Wikipedia, "Dual_EC_DRBG", https://en.wikipedia.org/wiki/Dual_EC_DRBG, 2017-01-02
Wikipedia, "Salsa20" (from which Chacha20 is derived), https://en.wikipedia.org/wiki/Salsa20, 2017-11-07
Wikipedia, "SHA-1", https://en.wikipedia.org/wiki/SHA-1, 2017-02-15
Wikipedia, "Trusted Platform Module", https://en.wikipedia.org/wiki/Trusted_Platform_Module, 2017-02-17
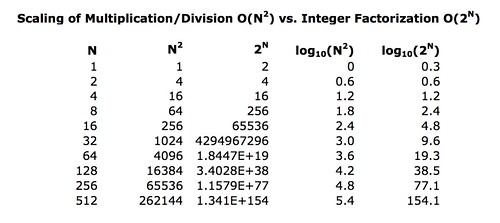
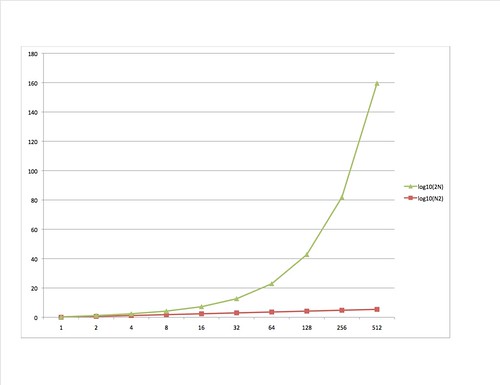

No comments:
Post a Comment