First-Come First-Served Readers and Writers in C using Monitors

And so it came to pass that I needed a solution to the Reader-Writer Problem using POSIX threads and written in C. So that there would be a consistent perception of reality amongst the components of a real-time system, it would be required that the Readers and Writers be given access to the shared resource in the strict order in which their requests were made. So it was, in the fullness of time, I developed such a solution. And I found it was good.

The Reader-Writer Problem

The Reader-Writer Problem (or, sometimes, the Readers-Writers Problem) is a classic concurrency problem in computer science. I studied it in school in the 1980s, but papers were being published about it in the early 1970s, just as computers were large enough to actually run more than one program at a time, and shared databases were becoming commonplace.

A Reader is any algorithm that needs read-only access to a shared resource. That shared resources could be a persistent database, a complex data structure in memory, or just a variable. A Writer is any algorithm that needs read-write access to the same shared resource. The Reader-Writer Problem is all about how you keep Writers from stepping on each other and on Readers as they modify the shared data.

The classic example of this in all the introductory textbooks is your bank balance. An algorithm in the bank computer, Writer A, wants to see if you have enough money in your bank account to cover your ATM withdrawal of $200. It reads your balance, and sees that you have a balance of $500, and tells the ATM to give you your money. Meanwhile, Writer B want to see if you have enough money to cover a check for $400 drawn against your account. It reads your balance, sees that you do, and clears the check. Writer A deducts the $200 from your account. Writer B deducts the $400 from your account... and now you see the problem.

(The thing is: this actually happens all the time. The global banking system is distributed across a huge number of computers, and verifying every single transaction in real-time is too expensive and time consuming. The banking system reconciles all of the transactions at best at the end of the day. So sometimes you overdraw your account. But it works as an introductory example.)

So clearly the act of checking your balance and deducting the money needs to be done as an atomic, or indivisible, operation - without the balance being changed in the middle of the transaction. Hence, only one Writer can run at a time.

If all an algorithm is doing is reading - a Reader that just checks your bank balance - that is an operation that can be done concurrently with other read-only operations. Readers don't step on one another, and many Readers can run at the same time. For reasons of efficiency, there is no reason to block a Reader if only other Readers are running.

A Writer can step on a Reader, too. Perhaps a Reader accesses a shared account database to verify two separate things: that the password that was typed in matches the (probably encrypted) password in the database, and that the login entered has access to the specific resources that the user is trying to use. Both requirements must be met for the login to succeed, but the data that needs to be verified must be accessed in two different read operations. In between those two separate operations, a Writer steps in and processes a Change Password request. The result is that the Reader grants access, even though the password typed in was actually incorrect at the time access was granted.

(That probably happens all the time, too.)

So while multiple Readers can access a shared resource concurrently, Writer access must be serialized - only one Writer can access it at a time - and Readers have to wait until a Writer has completed and vice versa. Note how this is different than just placing each access of the resource, regardless of read-write semantics, inside a critical section protected by a mutex or a semaphore: that would unnecessarily serialize Readers' access as well as that of Writers. If most access is reading - which typically is the case - a Reader-Writer lock is far more efficient than a simple mutex.

Those are the basic rules, or invariants, for the Reader-Writer Problem. But typical solutions to the Reader-Writer Problem are more complicated than that. For example, if you have a constant stream of Readers, the simplest solution to the Reader-Writer Problem starves Writers; they are constantly blocked from modifying the shared resource as long as Readers keep requesting access, because the simplest solution gives Readers priority.

This doesn't really serve Readers either, since presumably a Reader wants the most up-to-date information in the database. Starving Writers really means that the data is old and effectively out of date with respect to the real-world - you have written a lot of checks that have not yet cleared, so your bank balance reflects what an accountant would call its cash basis, not its accrual basis. That makes the data the Readers are reading a lot less practically useful.

Likewise, giving Writers priority can starve Readers if there is a constant stream of Writers wanting to modify the shared resource. That's not useful either, since you have a database with a lot of up-to-date information that Readers cannot access.

So you have to have a balance. The devil is in the details, which is why there are a lot of different solutions to the Reader-Writer Problem, all maintaining the same basic invariants regarding the integrity of the shared resource, but with different scheduling and policy decisions for Readers and Writers. Each solution is designed to meet the requirements of some specific application, or exhibit some specific behavior, like Readers are given priority as long as Writers don't wait longer than some timeout period, establishing a kind of "best if used before" date on the shared data.

And so we come to the requirements for my solution.

My Reader-Writer Problem

I had some specific needs for my solution. Not only did I need to meet the basic invariants of the Reader-Writer Problem, I needed the requests by Readers and Writers to be performed in the time order in which they occurred. Readers can run concurrently, but as soon as a Writer waits for the Readers to complete, all further Readers have to wait. More importantly (and the thing that was the departure from many Reader-Writer solutions), subsequent Readers and Writers that wait must be granted access to the shared resource in the order in which they made their request.

For example, if the order of arrival of Readers (R) and Writers (W) were in the following time ordered sequence (from left to right)

R₁ R₂ R₃ R₄ W₁ W₂ R₅ R₆ W₃ R₇ W₄ R₈

• R₁, R₂, and R₃ would all immediately be granted concurrent access;
• then W₁;
• then W₂;
• then R₅ and R₆ could run at the same time;
• then W₃;
• then R₇;
• then W₄;
• then finally R₈.

Other Reader-Writer algorithms may exhibit higher throughput for Readers, or for Writers, but this approach provides a more consist view of "causality", so that a post-hoc analysis of real-time system behavior agrees with the accepted perception of the order of events. I say "more consistent" and "accepted order" because a perfectly consistent view is impossible. I've written about this in my "Frame of Reference" blog articles, essentially applying Einstein's Theory of Special Relativity to real-time systems. (Computer scientist Leslie Lamport beat me to this idea by more than forty years.)

My Reader-Writer Solution

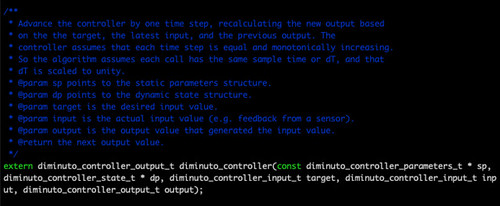
My solution is implemented in C under Linux using the GNU C library's implementation of POSIX threads, mutexen, and condition variables (and is different in implementation and probably behavior from the pthread_rwlock_t that POSIX provides - POSIX isn't that clear about how it behaves). You can find the source code in my Diminuto C systems programming library, whose Git repository is hosted on GitHub. Or you can follow the links below just to take a quick look at it right now.

diminuto_readerwriter.h

diminuto_readerwriter.c

unittest-readerwriter.c

The POSIX mutex and condition variable features together implement a form of synchronization originally referred to as a "monitor", as distinct from the earlier synchronization primitive, the "semaphore". Specifically, POSIX implements a Mesa monitor, whose behavior matches that of the monitors implemented in the Mesa programming language developed at Xerox PARC in the 1980s. Mesa monitors differ somewhat from the behavior of the original monitors described by C. A. R. Hoare several years earlier. I won't describe the POSIX mutexen or condition variables in detail, or either Mesa or Hoare monitors, but the references can be found below.

The one detail I do need to point out is that POSIX condition variables - a kind of queue on which threads can wait until another thread signals them to resume execution - do not guarantee First-In First-Out (FIFO) order: the order in which threads awaken on a condition variable can be completely different from the order in which they originally waited. POSIX condition variables are not guaranteed to be first come, first served. The order may be be affected by the scheduling priority that the application assigns to each thread, or it may depend on some specific detail of the underlying implementation. In any case, it is undefined in the POSIX 1003.1 specification. That was a problem I had to solve.

(There has been so much published on the Reader-Writer Problem over the decades that I would never claim that this solution is novel. It has undoubtedly been done before, and probably better. But a working implementation in the hand is worth two articles in the unread academic literature.)

(Update 2021-01-04: I found another, earlier, and very different implementation, by Shlomi Fish, which I added to the references at the end.) 

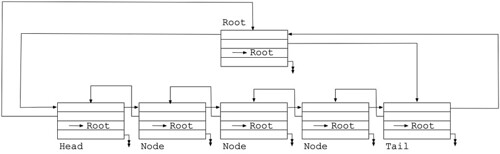
My solution uses one POSIX mutex, two POSIX condition variables (reader and writer), two counters that track the number of active Readers and Writers (reading, which should always be zero or greater, and writing, which should always be zero or one), and a queue used to store tokens (ring, which I implement as a ring or circular buffer).

(Update 2022-01-27: Diminuto library versions 74 and later do not require that the application provide storage for a ring buffer. The ring buffer is replaced by a diminuto_list_t, a doubly-linked "wait list", that is provisioned automatically and managed internally. The parameters to diminuto_readerwriter_init that provide a pointer to the ring buffer and its size have been eliminated. All other details remain the same.)

Once the Reader-Writer lock has been initialized, there are only four basic operations: a Reader can request access, a Reader can relinquish access, a Writer can request access, and a Writer can relinquish access.

Reader Request

When a Reader requests access and there are no active Writers (writing is zero) and there are no tokens on the ring, the reading counter is incremented and the Reader is granted access.

When a Reader requests access and there is an active Writer (writing is one), or if there are tokens on the ring, the Reader appends a READER token (indicating a waiting Reader) to the tail of the ring and waits on the reader condition variable.

When a waiting Reader wakes up, it checks to see if its token is at the head of the ring, and that it has been changed to READING (indicating a ready Reader). If both are true, it removes its token from the head of the ring, and proceeds to access the shared resource. (As we shall soon see, the reading counter will have already been incremented. This is important so that newly arriving Readers or Writers will not see the reading or writing counters as zero before the awakened thread has had time to reacquire the mutex.) If not, it waits again on the reader condition variable.

Just before a Reader exits the critical section that surrounds the Reader request mechanism, it checks to see if there is waiting Reader as the head of the ring. If there is, the exiting Reader changes the token at the head of the ring from READER to READING, increments the reading counter, and broadcasts a signal that wakes up all of the Readers on the reader condition variable. We have to use the broadcast POSIX function - which wakes all waiting threads - instead of the signal POSIX function - which wakes one waiting thread - because we don't know in what order threads will be awakened by POSIX, since FIFO order is not guaranteed.

Reader Relinquish

When the Reader relinquishes the shared resource, it first decrements the reading counter. If the reading counter is not zero, it is done. If the reading counter is zero (indicating there no other concurrent Readers), the relinquishing Reader checks to see if there is a waiting Reader or a waiting Writer by looking for a token at the head of the ring.

If there is a waiting Reader, the relinquishing Reader changes the token at the head of the ring from READER to READING, increments the reading counter, and broadcasts a signal that wakes up all of the waiting Readers on the reader condition variable.

Similarly, if there is a waiting Writer, the relinquishing Reader changes the token at the head of the ring from WRITER to WRITING, increments the writing counter, and broadcasts a signal that wakes up all of the waiting Writers on the writer condition variable.

Writer Request

When a Writer requests access and there are no active Readers or Writers (both reading and writing are zero) and there are no tokens on the ring, the writing counter is incremented and the Writer is granted access.

When a Writer requests access and there are one or more active Readers, or an active Writer, or there are tokens on the ring , the Writer appends a WRITER token to the ring and waits on the writer condition variable.

When a waiting Writer wakes up, it checks to see if its token is at the head of the ring  and that it has been changed to WRITING. If both are true, it removes its token from the head of the ring,  and proceeds to access the shared resource. If not, it waits again on the writer condition variable.

Writer Relinquish

When the Writer relinquishes the shared resource, it first decrements the writing counter. It then checks to see if there is a waiting Reader or a waiting Writer by looking for a token at the head of the ring.

If there is a waiting Reader, the relinquishing Writer changes the token at the head of the ring from READER to READING, increments the reading counter, and broadcasts a signal that wakes up all of the waiting Readers on the reader condition variable.

Similarly, if there is a waiting Writer, the relinquishing Writer changes the token at the head of the ring from WRITER to WRITING, increments the writing counter, and broadcasts a signal that wakes up all of the waiting Writers on the writer condition variable.

Practical Matters

The variables for the Reader-Writer lock are baked into a structure that has its own type definition.

diminuto_readerwriter_t lock;

The structure contains the mutex, the two condition variables, the counters, and the metadata for the ring buffer; the actual storage for the ring buffer is provided by the application in the form of an array that is at least as large as the maximum number of threads that may use the lock at any one time. Each slot in the array is just one byte. No initialization of the array is necessary. (My implementation doesn't have to do any initialization of the array either; the ring buffer metadata insures that the implementation never examines an uninitialized slot in the array.)

(Update 2022-02-01: In addition to the initialization function shown below, Diminuto library versions 74 and above also provide a mechanism for static initialization of the ReaderWriter lock structure. This allows the structure to be automatically initialized by the C run-time static initialization when an application starts.)

There is a function that initializes the ReaderWriter lock structure.

uint8_t ring[64];

diminuto_readerwriter_init(&lock, ring, 64);

Using the Reader-Writer lock is probably the simplest part, since all the necessary code is generated by C preprocessor macros that implement a "bracketing" pattern. These let you use the Reader-Writer lock like this, for Readers:

DIMINUTO_READER_BEGIN(&lock);

/* Read the shared resource here. */

DIMINUTO_READER_END;

or like this, for Writers:

DIMINUTO_WRITER_BEGIN(&lock);

/* Read and write the shared resource here. */

DIMINUTO_WRITER_END;

If one of the underlying POSIX functions fails for some reason (the most likely reason for this is the developer forgot to initialize the lock structure), the section of code bracketed by the macros is not executed. There is no error indication to the application, but it is a simple thing for the application to check that the code was executed. The implementation logs error messages either to standard error, or to the system log if the application has no controlling terminal i.e. is a daemon, so failures are not silent.

Discussion

Why two condition variables, one for Readers, and another for Writers?

Although I haven't tested it, my algorithm should work just fine having all of the waiting threads queued on a single condition variable. The waiting Readers and Writers don't depend on what condition variable they wake up on to know whether they've been granted access to the shared resource. There could be one token indicating READY that the head of the ring is set to, whether from a READER or from a WRITER, instead of the two different ready tokens, READING or WRITING. I think the only difference would be more churn amongst signaled Readers and Writers until all but one thread, the one whose token is at the head of the ring, go back to waiting.

Another approach would be to make every slot in the ring a condition variable. Each waiting thread would wait on its own dedicated condition variable. The signaling thread could signal instead of broadcast, since there would be no ambiguity as to which thread was being woken up. My only concern about this would be the resource usage involved.

I'm not unhappy about my design, so I'm not likely to change it. Using two condition variables seems efficient enough, and using a condition variable per slot in the ring doesn't seem necessary.

My design orders the access to the shared resource independently of the priorities of the calling threads, so it can result in priority inversion (but to not to do so would violate my own requirements).

One of the capabilities I have thought about adding is an optional timeout on the request for Readers and Writers, using a POSIX timed wait. I'm not completely convinced that there is a use case for this, except perhaps when recovering from some failure; how many algorithms have a credible Plan B if the request for the lock times out? It would also require that tokens in the middle of the ring be capable of being be rescinded. This is a lot harder than it sounds. Either the ring needs to be converted into something like a Diminuto List, a circular doubly-linked list (which would greatly increase the size of each slot from one byte to four pointers); or the maximum size of the ring can no longer be calculated (a Reader or Writer may timeout many times, each time adding a token to the tail while leaving an old token on the ring waiting to be removed at the head). I'm still pondering this.

(Update 2021-01-07: And I ultimately implemented the timeout, in part because it made it easier to test the recovery from certain failure scenarios. The timeout is available in the public function API, but not in the wrapper macros. You can find examples of both uses in the unit test. A timeout duration of zero provides a way for the application to poll for the availability of the resource.)

(Update 2022-01-30: As mentioned above, I finally replaced the ring buffer with a Diminuto List. The List node for each thread is automatically dynamically allocated in the thread's local storage and initialized on its first use. It is automatically de-initialized and freed when the thread exits.) 

(Update 2022-01-30: Diminuto library versions 75 and above support an expedited access request which queues the requesting thread at the head of the wait list instead of at the end. This provides a broad variety of alternatives in terms of how threads are scheduled to use the resource.) 

My Diminuto library and the results of its Reader-Writer solution should be pretty easy to reproduce on any modern Linux/GNU system. If this is the kind of thing that overclocks your processor, try it out. Clone the repository. Build the code base. Run the unit test. Peruse the code. See what you think. The unit test has passed on an x86_64 Ubuntu 18.04 platform, and on an ARMv8 Raspian 10 platform.

(Update: I made minor edits, and additions to the Discussion section, since I first posted this.)

For Further Reading

Wikipedia, "Readers-writers problem", 2020-11-23

Wikipedia, "Readers-writer lock", 2020-11-16

C. Overclock, "Frames of Reference IV", 2020-05-22

C. Overclock, "Frames of Reference III", 2020-01-28

C. Overclock, "Frames of Reference II", 2018-04-19

C. Overclock, "Frames of Reference", 2018-03-14

pthread_cond_timedwait, pthead_cond_wait, Open Group Base Specification Issue 7, 2018 edition, IEEE Std. 1003.1-2017, 2018

pthread_cond_broadcast, pthead_cond_signal, Open Group Base Specification Issue 7, 2018 edition, IEEE Std. 1003.1-2017, 2018

S. Fish, "A First-Come First-Served Readers/Writers Lock", 2009-04-18

B. Lampson, D. Redell, "Experience with Processes and Monitors in Mesa", Communications of the ACM, 23.2, 1980-02

L. Lamport, "Time, Clocks, and the Ordering of Events in a Distributed System", Communications of the ACM, 21.7, 1978-07

C. Hoare, "Monitors: An Operating System Structuring Concept", Communications of the ACM, 17.10, 1974-10

P. Courtois, F. Heymans, D. Parnas, "Concurrent Control with ''Readers'' and ''Writers''", Communications of the ACM, 14.10, 1971-10

Old Dog, New Tricks

In their article "File Descriptor Transfer over Unix Domain Sockets" in their blog CopyConstruct, distributed systems engineer Cindy Sridharan references an article by Facebook engineers and others that appeared in the proceedings of a virtual ACM conference: "Zero Downtime Release: Disruption-free Load Balancing of a Multi-Billion User Website" [Usama Naseer et al., SIGCOMM '20, 2020-08-10]. It's a real eye opener. I thought I was pretty conversant with the socket interface available in Linux, having been doing that kind of interprocess/interprocessor communication since my 4.2 BSD days on a VAX-11/750. Apparently I have some catching up to do.

Sridharan's article points out that you can transfer open sockets from one process to another, running on the same computer, via a UNIX domain socket, in the address family AF_UNIX (a.k.a. AF_LOCAL). UNIX domain sockets (or what I typically refer to as "local sockets") only work between endpoints on the same computer. Instead of using an IP address and port number, the rendezvous between endpoints is identified using a unique name in the file system namespace. Local sockets are have been around for eons, but I was not aware of this use for them.

What this is not is a child process inheriting a file descriptor from a parent process. This is sending a message over a local socket from one process to another that effectively results in a dup(2) system call on the receiving end for one or more file descriptors from the sending end that are specified in the message. The system calls involved are sendmsg(2) and recvmsg(2).

ssize_t sendmsg(int sockfd, const struct msghdr *msg, int flags);

ssize_t recvmsg(int sockfd, struct msghdr *msg, int flags);

Even the socket type was a new one on me: SOCK_SEQPACKET, which exchanges a message having fixed boundaries like a datagram, but which has guaranteed delivery like a TCP socket.

int listensocket = socket(AF_UNIX, SOCK_SEQPACKET, 0);

I had used sendmsg and recvmsg with struct msghdr before, to send and receive vector I/O using datagrams. You can find examples of this in my test program unittest-ipc-scattergather.c that I described in a previous article "Scatter/Gather".

But struct msghdr has additional fields that can be used to transmit additional ancillary information (the term used in the manual page). This includes control messages like SCM_RIGHTS, which enables the transfer of open file descriptors across process boundaries. (You still have to transmit at least one byte of conventional data, even if it is ignored by the far end; the control message tags along.)

You can find the test program described here at unittest-ipc-ancillary.c. In that program, there is one "main" process, one "workload" process, and four "instance" processes. 

The workload process manages a pool of sixty-four client threads. Each active client thread is trying to connect to the same listen socket identified by an IP address and port number. When the connection is established, the client writes one or more requests, and for each request reads a response from the server on the far end. Then the client closes the connected socket, returns itself to the thread pool, and ends. The workload process continuously waits for a client thread to appear in pool; it removes it from the pool and starts it.

Each instance process uses sendmsg to send a message to the main process over a local socket asking for the listen socket. The listen socket is a conventional socket identified by an IP address and port number, and has pending client threads waiting for their connection to be accepted. The main process receives the request using recvmsg and replies using sendmsg with its open listen socket to one instance process at a time until that process exits and its status is waited for by the main process. Then the connection request of the next instance process is accepted, and it is sent the same open listen socket.

Each instance process manages a dispatcher thread. The dispatcher thread continuously accepts connection requests on the listen socket from client threads, and assigns each new stream socket to one of eight server threads that it has started from a thread pool. When the client thread closes its end of the socket, the server thread returns itself to the thread pool and ends. During a single activation, a server thread services a sequence of requests from a single client.

The main process that drives the test gives each of the eight instance process ten seconds to service as many clients as it can before it is signaled by the main process to exit.

Here is a code snippet lifted from that test program for the sending side. diminuto_ipcl_packet_send() is the function in my Diminuto library that calls sendmsg.

struct iovec vector[1];

struct msghdr message;

union { struct cmsghdr alignment; char data[CMSG_SPACE(sizeof(int))]; } control;

struct cmsghdr * cp;

char dummy[1] = { '\0' };

 

vector[0].iov_base = dummy;

vector[0].iov_len = sizeof(dummy);

message.msg_iov = vector;

message.msg_iovlen = countof(vector);

message.msg_control = &control;

message.msg_controllen = sizeof(control);

cp = CMSG_FIRSTHDR(&message);

cp->cmsg_level = SOL_SOCKET;

cp->cmsg_type = SCM_RIGHTS;

cp->cmsg_len = CMSG_LEN(sizeof(listensocket));

memcpy(CMSG_DATA(cp), &listensocket, sizeof(listensocket));

ASSERT(diminuto_ipcl_packet_send(activationsocket, &message) == sizeof(dummy));

Here is a code snippet from the receiving side. Similarly, diminuto_ipcl_packet_receive() calls recvmsg. Note that the value returned by both sendmsg and recvmsg is the length of the dummy payload, not the length of struct msghdr or struct cmsghdr.

char dummy[1];

struct iovec vector[1];

struct msghdr message;

union { struct cmsghdr alignment; char data[CMSG_SPACE(sizeof(int))]; } control;

struct cmsghdr * cp;

ssize_t length;

int listensocket = -1;

 

vector[0].iov_base = dummy;

vector[0].iov_len = sizeof(dummy);

message.msg_iov = vector;

message.msg_iovlen = countof(vector);

message.msg_control = &control;

message.msg_controllen = sizeof(control);

ASSERT((length = diminuto_ipcl_packet_receive(activationsocket, &message)) == sizeof(dummy));

for (cp = CMSG_FIRSTHDR(&message); 

     cp != (struct cmsghdr *)0; 

     cp = CMSG_NXTHDR(&message, cp)) {

  if (cp->cmsg_level != SOL_SOCKET) { continue; }

  if (cp->cmsg_type != SCM_RIGHTS) { continue; }

  if (cp->cmsg_len != CMSG_LEN(sizeof(listensocket))) { continue; }

  memcpy(&listensocket, CMSG_DATA(cp), sizeof(listensocket)); break; 

}

The test program is constructed such that the listen socket being passed to each instance process doesn't even exist when the instance processes are forked. The only way the listen socket could be known to the instance processes is via the control message mechanism.

This is a remarkable capability. I own Cindy Sridharan a debt of gratitude for bringing it to my attention.

Addendum (2020-12-15)

Fazal Majid was kind enough to pass along the fact that this capability has been around for a long time, and cited a classic reference that I have on my bookshelf just a couple of feet away.

W. Richard Stevens, Stephen A. Rago, Advanced Programming in the UNIX Environment, 2nd ed., Addison-Wesley, 2005

It took me a few minutes to find it: 17.4.2, "Passing File Descriptors over UNIX Domain Sockets", pp. 606-614. I'm embarrassed to admit I missed this. In my defense, the book is 927 pages long. A big thank you to Mr. Majid for pointing this out.

Addendum (2020-12-16)

The SOCK_SEQPACKET socket type looks pretty interesting, doesn't it? It has the reliability of SOCK_STREAM with the fixed message boundaries of SOCK_DGRAM. Why don't we see it used more? Because underneath the hood it uses neither the Transmission Control Protocol (TCP) used for streams, nor the User Datagram Protocol (UDP) used for datagrams, the two transport-layer protocols on which most of the Internet is based. Instead, it uses the Stream Control Transmission Protocol (SCTP) developed for Signaling System 7 (SS7), the telecommunications protocol stack used to set up and tear down telephone calls in the Public Switched Telephone Network (PSTN). SCTP is defined in RFC 4960. SCTP isn't as widely deployed in the Internet at large as its peers in the transport layer. I'm not confident SCTP packets would make it through all firewalls. And it's not that hard to parse out fixed size messages from TCP streams. Diminuto provides an API to create a sequential packet socket only for the UNIX domain (local) address type, where it might be useful for inter-process communication on the same computer.

Scatter/Gather

The Linux kernel has a variety of I/O system calls that can be used to write data to and read from a file, device, or network. Which system call you use depends in part on how you want to treat the data, for example as as an unformatted (to the kernel anyway) stream of bytes, or as a fixed length datagram. Recently I was reminded of the readv(2) and writev(2) system calls, which read and write vectors of data which reside in non-contiguous areas in memory.

(Click on any image to see a larger version. Or any version of all, since Blogger doesn't alway play well with Flickr.)

These calls take, not a pointer to a buffer and a length in bytes, as is typical of other I/O system calls, but a pointer to an array known as an I/O vector (not to be confused with an interrupt vector), and a count of the number of positions in the array. (The readv and writev system calls are for streams; there are similar system calls, recvmsg(2) and sendmsg(2), that you can use for datagrams.)

Every array position in the I/O vector is an iovec structure. Each iovec structure contains a pair of fields: a pointer to the data to be written or a buffer into which data will be read, and the length in bytes of the data to be read or written.

I take it from the comments in the header file that readv and writev were originally adapted from the Berkeley Software Distribution (BSD), a UNIX variant I cut my teeth on decades ago on a DEC VAX-11/750. But it was later, at the National Center for Atmospheric Research in Boulder Colorado, where I was introduced to vector I/O, which was used to read and write ginormous lists of floating point numbers used in the specialized vector supercomputers at that national lab. Those high performance machines could do many identical floating point operations in parallel on those data vectors, multiplying and dividing dozens of numbers together all at once. I'm told vector I/O also has its place in high performance graphics hardware.

But my interest in vector I/O comes from the many years I've spend working in protocol stacks for technologies, like Asynchronous Transfer Mode (ATM) and cellular base stations, in the telecommunications industry.

Vector I/O

Supposing you want to transmit a packet whose wire format - what it looks like as it is transmitted over the network, not necessarily what it looks like in memory - looks like this. (This is a pretty simple example compared to typical network protocols.)

The wire format has five fields: a four-byte IPv4 address, a two-byte port number, an eight-byte payload length (which would be overkill for sure), a variable length payload, and finally a two-byte (sixteen-bit) checksum.

These fields may not be in a contiguous location in memory in the protocol stack. In fact, because of memory alignment requirements for the different fields, it may be impossible for them to be contiguous without copying each field byte by byte into a buffer as character data. Furthermore, the way protocol stacks are designed, these fields are probably not managed by the same software layers. By way of a trivial example, when creating an outgoing packet: one layer dealing with the application and business logic generates the payload; another layer responsible for packaging the payload and insuring it arrives intact adds the length field to the beginning and the checksum to the end; and a third layer whose duty is to route the data to the recipient adds the address and port number to the beginning.

One way I've seen this handled in production software is to do a lot of data copying and recopying. That tends to be expensive in terms of time and memory usage. Another way (which I thought was pretty clever, I wish I'd thought of it) was to use double-ended buffers: a single buffer was passed through the layers, the application put its payload more or less in the middle of the buffer, and each successive layer prepended and appended fields to either end. This still involves a lot of data copying from application variables into a contiguous buffer. I wondered if I/O vectors could be yet another approach to solving this problem.

You may have read or heard about zero-copy I/O. This is not that. Vector I/O is a way to eliminate copying in the application from variables to a buffer. Zero-copy I/O is a way to eliminate copying between user space where the application runs and kernel space where the device driver runs. For example: the application makes a zero-copy system call to write a buffer out to a device, file, or network. Instead of making a copy of all the application data from user space to kernel space and then releasing the application buffer, the kernel instead takes ownership of the application buffer, and later asynchronously notifies the application that the I/O is complete. The application can't mess with its own buffer until this notification arrives. It's possible to use both vector I/O and zero-copy I/O to avoid both types of copying (although my test program doesn't do that).

The application using writev instead populates an iovec array with pointers to, and the lengths of, each data field. When the data is ready to be written onto the wire (file, device, or network), the writev system call steps through the array and writes each field one by one in order. (The Linux implementation makes sure this operation is atomic, so a writev running in one process or thread can't intermingle fields with another concurrent writev.)

For our example packet above, the iovec array would look like this.

Vector reads work similarly: the application using readv prepares an iovec array containing empty buffers and their lengths into which data will be read.

That's why this technique is sometimes referred to as scatter/gather: data read serially off the wire is scattered into separate memory locations instead of into a single contiguous buffer; data written to the wire is gathered from separate memory locations and serially written onto the wire.

I wanted to try out the various vector I/O system calls in Linux, so I wrote a little program to do just that. But I didn't want to do anything as prosaic just using iovec arrays. That would be too simple. I decided instead to try out an idea I've had for a long time: using a linked list to pass the data through the various software layers of a simulated protocol stack. And not any linked list, but the doubly-linked diminuto_list_t data structure I implemented in my Diminuto C systems programming library many years ago.

Lists

The Diminuto List implements a doubly-linked list - a linked list in which each node has a pointer to the next item on the list, as with a singly-linked list, and a pointer to the previous item on the list.

(You can find the source code for the Diminuto List implementation on GitHub at diminuto_list.h and diminuto_list.c.)

Singly- and doubly-linked lists are familiar to anyone who has taken Data Structures 101. Doubly-linked lists have an advantage over singly-linked lists in that a node can be removed or inserted anywhere on the list. Diminuto Lists (or just Lists, with a capital L, for brevity) have a few other features besides the next and previous links.

Each node on a List also has a link to the root of the list. This means that given any node on a List, you can find out what List it's on without traversing the List back to the root. So you can do things like trivially prepend or append a new node onto the same List as another node.

Diminuto Lists don't use null pointers, except for the data payload pointer, or as a returned value to indicate a specific condition. Lists are circular doubly-linked lists. The previous pointer on the node at the head of the List points back to the root note; the next pointer on the node at the tail of the List also points back to the root node. You know a node is at the head of the list because its previous pointer and its root pointer are the same. Similarly, a node is at the tail of the list because its next pointer and its root pointer are the same. When you insert a new node onto a List, that node inherits the root pointer from the node after which it was inserted.

Every Diminuto List node has a void * pointer that can point to a data payload. You can use this field by allocating nodes and payloads separately, and have each node point to its corresponding payload, whatever that is. Or you can embed an diminuto_list_t node structure as a field in the payload structure itself, and either ignore the data pointer, or use it to point to the beginning of the payload. You can have multiple node structures in a payload structure, so that the payload can exist on multiple Lists simultaneously; each node's payload pointer can point to the beginning of the containing structure; this eliminates the need to know which node structure you are using in a payload structure in order to compute the address of the beginning of the payload structure.

The root of a Diminuto List is just another node. You know it's the root node because its own root pointer is pointing to itself. Your application may choose to use the payload pointer in the root node for something, or just ignore it.

When a List node is newly initialized it looks like this.

The node's next pointer, its previous pointer, and its root pointer are all pointing to itself. It is in effect the root of an empty List. Whether it remains a root node depends on whether another node is inserted onto it (then it is), or it is inserted onto another List (then it isn't).

As you insert nodes, the next and previous pointers in the inserted node and the adjacent nodes, as well as the root pointer in the inserted node, are all adjusted appropriately. Similar when you remove a node. Because a List is circular, there are no special cases about inserting, removing, appending, or prepending, a node on a List. And you can splice an entire List into another List; the root pointers in the spliced List will all be rerooted to point to the root of the List onto which it is being spliced. You can cut out a sub-List from an existing List, and reroot that new List to a new root node.

If you have a Diminuto List with five nodes plus the sixth root node, it looks like this. (I abbreviated the root node pointers so as to not make the diagram too tangled.)

I don't use Diminuto Lists for everything: the overhead of the four pointers is overkill for applications where one suffices. But they have proven remarkable flexible. So it seemed like a good idea for this experiment.

Gather

The idea here is that different layers in the protocol stack incrementally build a packet by putting the value of each field to be transmitted into a payload buffer associated with a List node, then prepend or append (or even insert or replace) that node onto a List that will eventually represent the entire packet. When the packet is completely built, the application hands off the root node to a function which walks the entire List to build an I/O vector, and then passes the vector to a system call to put on the wire. 

(You can find the source code for this test program on GitHub at unittest-ipc-scattergather.c.)

The highest layer of the stack puts a node whose data payload pointer points to a buffer containing the data to be transmitted. In my test program, these buffers are allocated from a pool (as are the List nodes, from a different pool), and each buffer has a length field at its beginning. The start of the data field of a buffer from the pool is eight-byte aligned, so that its address can be cast to be a pointer of an application variable or structure; that pointer can be used via indirect addressing without copying values. In my test program, the root node is referred to as a record, and the nodes with payload buffers are called segments.

The record is, of course, initially empty. Once the payload segment is put on the record, the record looks like this.

The next layer of the stack prepends a segment at the beginning of the record that contains the length of the data to be transmitted in an eight-byte field. (The length is just taken from the length field in the payload segment's data buffer). It appends a segment to the end of the record that contains a two-byte Fletcher-16 checksum field that it computed from the payload data. The record now looks like this.

The record gets passed to another layer that prepends two segments to the beginning of the record: one containing a four-byte IPv4 address, and another containing two-byte port number.

The record gets passed to a final layer that interrogates the address and port segments of the record to get the destination to which the record is to be sent. It then passes the record along with this information to a function which vectorizes the record: the function just walks the List from front to back, interrogating each segment for a pointer to the beginning of its data buffer and the value in that buffer's length field. It shoves each of these pairs of data into successive positions in the I/O vector. (This is the same figure as seen above.)

It then calls the appropriate system call, writev(2) for streams or sendmsg(2) for datagrams, which puts the resulting serialized packet on the wire. (This is also the same figure as above.)

This completes the gather portion of the I/O. (With the appropriate abstraction and packaging into supporting functions, this was all a lot easier to code than it sounds.)

Scatter

The scatter portion of the I/O is almost the same operation, but done in reverse. But there is a complication: the payload portion of the packet is variable length, so the application has no way of knowing ahead of time what how large a data buffer to assign to the segment the represents that payload field, or what length to put in the I/O vector for the system call.

For datagram sockets, I solved this problem by having four segments, for four fields - address, port, length, and payload - instead of five. The last segment has a data buffer that is large enough to contain the largest possible payload and the two-byte checksum. The datagram receiver in the test program has to extract the checksum from the end of the payload buffer once the length is known. Because, like all good software developers, I'm a little OCD, I added the checksum as another segment which I appended to the record, and adjusted the length field in the payload data buffer by two bytes.

This solution doesn't work for stream sockets, because if there is a second packet behind the one we are receiving, the beginning of that packet would be read into the larger payload buffer past the data of the prior packet. I solved this problem by doing two vector I/O operations: the first reads the address, port, and length; once the length is known, the second reads the payload and the checksum. This solution isn't possible for datagram sockets, since datagrams are transmitted and received as a single unit.

Or you can ditch the entire vector I/O scheme on the receiving end completely. As my test program illustrates, the sender can transmit the packet using vector I/O, but the receiver can receive the packet using any appropriate scheme it wants. My test program implements a variety of ways of doing this for both stream and datagram sockets.

Remarks

I wrote the unittest-ipc-scattergather.c test program as a sort of audition for adding this kind of capability to the mainstream Diminuto library. I'm not convinced that it has broad enough applicability to make that worthwhile. But I rest easier knowing that I have a usable List-vector I/O scheme with a working example in my hip pocket.

Update (2021-03-19)

Today I made the scatter/gather capability a mainstream Diminuto feature. The function and type names have been changed to reflect the canonical Diminuto style. The feature now supports both IPv4 and IPv6 sockets. Additional unit tests have been added. The unit tests are now part of the sanity test suite for Diminuto. All sanity tests pass.

Is the Virtuous Cycle really that virtuous?

In October 2020 I wrote a longish article titled Layers about the layered implementation that emerged organically from the fifteen years (so far) of work I put into my Diminuto systems programming library that is the underlying platform for much of my C-based work. After thinking more about the "virtuous cycle" I described in that article - where feedback from actual use of Diminuto lead to its evolution and expansion and then subsequent use in even more projects (including some shipping products) - I added an afterword. Upon even more reflection, the afterword got longer and longer. Eventually I decided it merited its own short blog article. This is it.

I wonder from time to time whether I'm the only person still working in C. Then I see the TIOBE Index where C is the #1 most used programming language. I find this remarkable, since my years of PDP-11 experience eons ago lead me to still think of C as a kind of structured PDP-11 assembler language.

C places around fifth in other surveys, which seems about right to me. Although I find Rust challenging to work in, I couldn't criticize anyone for using it for systems-level work. And maybe using Go instead of Java for application work. And I like Python too for non-performance-sensitive high level work.

One of the things I find really mysterious is that organizations who work in C, GNU, and Linux don't seem to put any effort into making C easier, simpler, more reliable, and more productive to use. That's exactly what using Diminuto does for me. I'm not trying to talk C shops into using Diminuto. But but I am arguing that they should do something like what I do with Diminuto. And they could do a lot worse than looking carefully at the layered implementation approach I talk about in this article.

I believe this is another case of the cognitive bias towards prioritizing the short term over the long term. Putting code that is likely to be commonly useful in other projects into a reusable library, along with unit tests, is a pattern that has worked very well for me. But in organizations larger than my tiny one-person company, it requires that the folks managing the project and holding the purse strings see the long term value in that. For most project managers there is no long term. And certainly nothing worth spending resources - schedule and budget - outside of their immediate project and silo.

It also requires enough experience to know what is likely to be more generally useful in the long term; I haven't always gotten that right myself. And once you have a library that is used in multiple projects, changes and maintenance on that library requires more diligence and incurs a higher price, since it affects multiple code bases. An API change that breaks legacy code requires careful consideration indeed to balance the cost of breakage against the cost of technical debt.

Line managers and developers are typically not incentivized to think long term. Agile processes do not encourage this either. I find it hard to argue against this. It's easy to get side-tracked and take your eye off of the immediate goal. Long term thinking is the job of senior architects and upper management. And as I like to say: if you don't survive in the short term, there is no long term. It's just that in my tiny corporation, I'm both the line developer and the senior architect. I have to pay attention to the tiny details and the big picture.

Balancing short term and long term needs is a hard problem.

Layers

 "Either you design a layered architecture, or you'll wish you had."
-- Ken Howard, Ph.D., Bell Labs

When Colorado got hit recently with an early winter storm bringing several inches of snow and 10ºF temperatures before Halloween had even arrived, I found myself wearing four layers of clothing while shoveling my driveway. It gave me time to think about the software layers that developed organically in Diminuto,  my open source C library and framework that has been the basis of almost all of my personal projects, and some or all of which has found its way into several shipping products. It will become obvious I'm using the term layers here a little differently than you might have seen before when referring to software architecture or network protocol stacks.

History

My work on Diminuto ("tiny") started in earnest in early 2008, with portions of it borrowed from earlier work I did in C++ in 2005, and based on even older C code I wrote in 1994. I began with a physically large and relatively expensive Atmel development board with an ARMv4 processor, a chip that seems laughably underpowered compared to the current ARMv7 and ARMv8 offerings that are in your mobile phone. This board predated the Raspberry Pi (2012), and even the BeagleBoard (2008). Having spent years writing C and C++ code for one real-time operating system (RTOS) or another like VxWorks, I was experimenting with building a minimalist Linux-based system that could run comfortably on the (then) memory-limited ARM processor. My testbed consisted of:

• a custom Linux kernel configured with only those features I really needed;
• uClibc, a stripped down C library;
• BusyBox, that combines a bunch of commonly used Linux/GNU utilities into a single binary executable; and
• my C-based application.

(You can click on any image to see a larger version.)

Even though I was shooting for a tidy KonMari-style system that would make Marie Kondo proud, I still found it useful to organize some of my code into a library and set of header files. Even then it had occurred to me that I might reuse some of this stuff in another context one day.

Diminuto, and my work that used it, eventually migrated to more capable platforms, like the BeagleBoard.

And then to the first Raspberry Pi.

Eventually I found myself using later, even more powerful Raspberry Pis, and that Single Board Computer (SBC), with Diminuto, running on its Debian-based Linux/GNU distro, became my standard deployment platform for a lot of later projects, like Roundhouse, my IPv6 testbed.

I occasionally found myself porting Diminuto to more powerful platforms, like the Nvidia Jetson TK1 development board.

Diminuto played a key role in even more exotic projects, like building Astrolabe, my own stratum-0 NTP server using a chip-scale cesium atomic clock (CSAC).

Over the span of twelve years, Diminuto continued to grow organically in a kind of positive feedback loop, as the C library and framework became more useful than my quest for a tiny embedded Linux system. I would work a gig to develop some commercial product, and encounter a software feature in either the Linux kernel or the GNU library that I thought was useful - like the run-time loadable user-space modules that are used by the Asterisk open source PBX - and I would fold support for that feature, along with unit and functional tests and sometimes command line tools, into Diminuto. Or I would use some or all of Diminuto in some commercial development, and find some things in my code that didn't work so well, so I would fix it. And I would continue to leverage that growing base of reusable code in my own personal work.

Today Diminuto amounts to over 56,000 lines of C and bash code distributed amongst almost 350 files, implementing 84 different features and 38 different command line utilities, with 97 unit test programs and 28 functional test programs. It forms the underpinnings for almost all of my Linux/GNU-based personal projects in C or C++, like Hazer, my project that explores technologies like Differential Global Navigation Satellite Systems (DGNSS) and Inertial Measurement Units (IMU).

(To give you another way to think about this evolution, decades ago I started out using the Source Code Control System (SCCS) to manage my source code changes to the precursors to Diminuto. For Diminuto, I started out using the Revision Control System (RCS). Then I migrated to Concurrent Versions System (CVS). Then to Subversion (SVN). And finally Git, with the repository hosted on GitHub. There are pieces of Diminuto that came from that earliest work that have been managed by five different code management systems.)

Different people learn in different ways. I envy my friends and colleagues who can pick up a book on some new technology, read it, and claim to have learned something. (Liars.) I can only learn by doing. I'm a very hands-on student. (Which is why I also have git repositories of C++, Java, Python, JavaScript, Go, and Rust code.)

Working on Diminuto has been fundamental to my ability to learn not just new (to me) and evolving C, Linux, GNU, and POSIX features, but also to experiment with Application Program Interface (API) design. I've learned a lot about porting Diminuto between processor architectures (I use it almost daily on ARMv7, ARMv8, and Intel x86_64 machines), and between different versions of Linux and GNU, and even different operating systems and C libraries; in the past I've ported all or parts of it to uClibc, Cygwin, Android/Bionic, and MacOS/Darwin. It has given me a way to write useful code once, test it throughly, and then reuse it, either in my own projects or in products I've helped my clients develop. As much as I like being paid by the hour, there are more fulfilling things to do than to write the same underlying code over and over again.

Even though I have at times ported Diminuto to other platforms, it is not portable, nor is it intended to be. It is specific to Linux and GNU, and to the kinds of work that I am routinely called upon to do. I regression test changes only against relatively recent versions of the kernel and the C library.

As Diminuto evolved incrementally in its virtuous cycle, without really much of a long-term plan on my part, I none the less noticed that it had developed a layered architecture, driven by the needs of whatever I was using it for at the time. Maybe this was an accident, or maybe it's my forty-plus years of experience talking. But in any case, as my old friend and colleague at Bell Labs, Dr. Ken Howard, would surely remark, a layered architecture is a good thing.

Layers

Layer 0: Documentation

Like most software developers, I'm more interested in writing code than I am in writing documentation. But like most software developers of a certain level of experience, I have come to realize that I have to document my work, if not for others, then at least for myself.  Plus, documentation is its own reward: while writing comments I sometimes think: "Hey, wait a minute. That doesn't make any sense at all." It's like a one-person code review. Also, like other developers of a certain age, I've looked at code I wrote months or years ago and wondered: "What the heck does this even do? And WHY?"

Documentation for Diminuto (and for most of my other projects) comes in three flavors:

• blog articles like the one you are reading now;
• Wiki-style documentation like that in the Diminuto README; and
• Doxygen comments embedded directly in the code.

Doxygen is a software tool that takes your source code containing comments written in Doxygen's markup language, and produces (with a little help from other tools) documentation in the form of HTML pages, traditional UNIX manual pages, and PDF files.

Doxygen supports comments for files, functions, types, structures, variables, constants, preprocessor symbols, pretty much anything you can do in C. (Doxygen supports other languages as well.) The PDF reference manual for Diminuto currently runs to 784 pages! Of course, the resulting documentation is only as good as the Doxygen comments from which it is generated.

My approach is to document each Diminuto feature with Doxygen comments in its .h header file - the part of Diminuto that is publicly accessible even in a binary installation - which defines the API for that feature. Doxygen comments may also appear in .c translation units to describe functions that are not part of the public API.

Even if I never refer to the generated documentation, Doxygen provides a canonical comment format for documenting my code. I routinely use the Doxygen comments to remind myself how my own code works.

Layer 1: Types

As much as possible I use the standard pre-defined data types provided by GNU and Linux, like the following:

• size_t and ssize_t defined in <stddef.h>;
• fixed-width integer types like int32_t and uint64_t defined in <stdint.h>;
• bool defined in <stdbool.h>; and
• pid_t in <sys/types.h>.

But it quickly became clear that it would be a good thing to have some standard Diminuto types that could be used broadly across all feature implementations. The header file

"com/diag/diminuto/diminuto_types.h"

not only automatically includes the standard header files cited above, but also defines some types that are used in Diminuto, like:

• diminuto_ticks_t that holds the common Diminuto unit of time;
• diminuto_ipv4_t that holds an IP version 4 address;
• diminuto_ipv6_t that holds an IP version 6 address; and
• diminuto_port_t that holds an IP port number.

All the higher layers are based on these types.

(Why the long #include path above for the Diminuto header file? It's to make integration into other code bases easier. See Some Stuff That Has Worked For Me In C and C++.)

Layer 2: Logging

I wanted to write reusable C code that could be part of a command line tool, part of a system daemon, or even part of a loadable module that runs in kernel space. To do that, I had to abstract away the specific mechanism used to display error messages. The Diminuto logging API defined in the header file

"com/diag/diminuto/diminuto_log.h"

does that. It borrows its design from

• the standard syslog(3) interface;
• from the Linux kernel's printk interface;
• from Android/Bionic's logging mechanism; and
• even from non-C logging facilities like those I've used in Java.

Diminuto defines eight log levels, from highest to lowest severity:

• emergency;
• alert;
• critical;
• error;
• warning;
• notice;
• information; and
• debug.

Whether log messages are displayed or not is determined by an eight-bit log mask. The default value of the log mask is 0xfc, which enables all log messages except information and debug. The log mask can be set programmatically or from an environmental variable. As a special case, if the environmental variable, which is called COM_DIAG_DIMINUTO_LOG_MASK, has the value "~0", all log messages are enabled.

So far, this sounds pretty mundane. Here's the interesting part.

• If the log function call is compiled as part of a kernel module, the Diminuto log functions automatically revert to using the kernel's printk logging mechanism; each severity levels is translated to the appropriate printk level; and their emission is controlled as usual by the value of /proc/sys/kernel/printk.
• If the calling process is one whose parent is the init process a.k.a. process id 1 (this typically means the child process is a daemon that has been inherited by init), or if that process is the session leader (which typically means it has no controlling terminal on which to display a log message), the log function routes the formatted message to the standard syslog(3) API; its severity level is translated to the appropriate syslog(3) severity; and its emission can be controlled via the standard setlogmask(3). For most systems, this means the message will be passed to the syslog daemon (however that may be implemented) and written to a file such as /var/log/syslog.
• In all other cases,  the formatted message is written to standard error.

This vastly simplified the handling of log messages. It made Diminuto code much more easily reusable in a broad variety of contexts. The same function, using Diminuto logging, can be used in a command line utility or in a daemon; either way, output messages (in particular, error messages) will be handled appropriately. Some functions can even be used in the context of a kernel-space device driver. But more importantly, it helps insure that error messages - and, as we will see below, a lot of useful context for debugging - are not lost. Furthermore, the emission of each Diminuto log message is serialized under the hood by a POSIX mutex, insuring that messages from different threads in the same process don't step on each other in the error stream.

Layer 3: Errors

The standard function perror(3), defined in <stdio.h>, prints an caller-defined error message on standard error along with a system-defined error message associated with  the global variable errno, which is typically set by failing system calls and C library functions. For example, the code snippet

errno = EINVAL;

perror("framistat");

where EINVAL is an integer constant defined in <errno.h>, displays the message

framistat: Invalid argument

on standard error.

The code snippet

errno = EINVAL;

diminuto_perror("framistat");

on the other hand displays

2020-10-27T19:28:02.889470Z "nickel" <EROR> [25416] {7f981766e740} foo.c@3: framistat: "Invalid argument" (22)

on standard error, or logs it to the system log, as appropriate. (It is displayed as one line; the rendering here folds it up.)

Because diminuto_perror goes through the normal Diminuto logging mechanism, the message includes the date and time in UTC with microsecond resolution, the host name of the computer, the severity level, the process identifier of the caller, the thread identifier of the caller, the name of the translation unit, the source line within the translation unit, and even the numeric value of the error. 

The diminuto_perror API is defined in the header file

"com/diag/diminuto/diminuto_log.h"

and is part of the Diminuto log feature.

Layer 4: Assertions

The standard assert(3) function, defined in <assert.h>, evaluates a caller-specified scaler expression, and if the result of that expression is false, it displays an error message on standard error and ends the execution of the caller using abort(3) defined in <stdlib.h>.

foo: foo.c:2: main: Assertion `1 == 2' failed.

Aborted (core dumped)

The diminuto_assert API that is defined in the header file

"com/diag/diminuto/diminuto_assert.h"

does all that too, but it emits the error message using the Diminuto log feature, so all that logging goodness applies here too.

2020-10-27T19:48:15.562081Z "nickel" <EROR> [25564] {7f5ed5040740} foo.c@2: diminuto_assert(1 == 2) FAILED! 0=""

Aborted (core dumped)

(It also prints the value of errno, just in case it's useful to the developer debugging this failure.)

This is a lot more useful than it might first appear. Truth is, most serious errors - like error returns from systems calls - hardly ever happen, and if they do, they aren't typically realistically recoverable. A bunch of "error recovery" code often just serves to clutter up the source code, complicate testing and debugging, and add to the cognitive load of the developer. Most of the time, the best thing to do is to dump core and exit, and leave the recovery to higher minds - like the user sitting at the terminal, or maybe systemd. Using diminuto_assert can really clean up your code by reducing both error handling and error messaging to one function call.

Here's a tiny code snippet from the gpstool utility in my Hazer GPS project, which is built on top of Diminuto.

If the standard malloc(3) function fails to allocate memory, the entire program just goes toes up. Not a lot of drama, just an error message and a core dump, without a lot of other error handling code cluttering up the translation unit.

Layer 5: Unit Tests

I've used a lot of different unit test frameworks over the years for C, C++, Java, and Python development. The Diminuto unit tests didn't need a lot of complex support for mocking and what not. I wanted something dirt simple but functional. Most of all, I didn't want users of Diminuto to have to install an entirely different package to support the unit tests. So an almost trivial unit test frame became part of Diminuto itself. (And before you ask: yes, there is a unit test in Diminuto for the Diminuto unit test framework.)

Here is a code snippet that is one simple unit test from the suite that exercises the Diminuto InterProcess Communication (IPC) feature.

The unit test framework is nothing more than a series of C preprocessor macros. Here you can see that a new test is declared, a mixture of assertions (where failures are fatal) and expectations (where failures are logged and counted) are made, and the outcome of the test is displayed. If the unit test succeeds, the following is displayed.

2020-10-27T20:27:08.354153Z "nickel" <NOTE> [25741] {7fbabe66a000} tst/unittest-ipc.c@237: TEST: test=8

2020-10-27T20:27:08.354193Z "nickel" <NOTE> [25741] {7fbabe66a000} tst/unittest-ipc.c@246: STATUS: test=8 errors=0 total=0 SUCCESS.

The unit test framework API is defined in the header file

"com/diag/diminuto/diminuto_unittest.h"

and makes use of the Diminuto log feature.

Layer 6: Wrappers

Most of the features in Diminuto have fairly complex implementations. Some don't. Some are not much more than wrappers around system calls and C library calls. But for something that is used often, a little wrapping can lead to fewer surprises (contrary to the usual case with wrapping).

Consider the code snippet below, from the Hazer gpstool utility. 

You can see if the standard fopen(3) call fails, the error leg calls both diminuto_perror, which prints the name of the file that failed to open and also the error string corresponding to the errno set by fopen(3), and diminuto_assert, which core dumps the application.

Compare that to this code snippet, also from the Hazer gpstool utility,

in which only diminuto_assert is called.

Why the difference? Because the failing function in the second example is itself part of Diminuto. It already called diminuto_perror before it returned to the application. Even just having simple wrappers around frequently used system calls and library calls that automatically print an error message - using the smart Diminuto log-based features - reduces the amount of clutter in the source code of the application.

Of course, there maybe circumstances which the application should to print its own error message with more specific contextual information. But most of the time, the error emitted by the Diminuto code is sufficient.

Layer 7: Models

Why do some Diminuto features have complex implementations? Because they implement a specific model or design pattern of using a particular system call or C library facility. That model may have complex behavior. Typically the model is based on forty-plus years of hard won experience on my part on doing exactly this kind of thing. Or sometimes just on my opinion of the right way to do things. Or on horrifically tragic mistakes I've made in the past.

Here's an example that I already talked about in Timer Threads. Diminuto has a timer feature whose API is defined in

"com/diag/diminuto/diminuto_timers.h"

and which is based on POSIX timers. There is a potential race condition in POSIX timers between the application that starts (arms in POSIX-speak) and stops (disarms) a timer and the callback function that is invoked by the timer. POSIX timer callbacks run in a thread-like context - which is just a man page way of saying it is in fact a POSIX thread, separate from the application thread. When the application stops the timer, the callback may already be running, especially with a periodic timer, and on a multi-core (which these days is virtually any) processor. If the application releases resources - for example,  frees memory, or closes files - that it shares with the timer callback function, that function can have those resources pulled out from under it. Wackiness ensues.

Diminuto incorporates a POSIX mutex and condition in every Diminuto timer. When the application calls the Diminuto function to stop the timer, the function calls the POSIX function to stop the timer (not shown below), enters a critical section, indicates to the timer callback that it is placing it in a disarmed state, then waits for the timer callback to acknowledge it.

When the Diminuto timer callback (a private proxy function that invokes the user-specified callback) has finished its current business, it enters a critical section, checks to see if it has been disarmed, and if so, acknowledges that fact and signals the waiting application.

This prevents the race condition. This is some fairly complicated stuff, and it's all transparent to the application.

What if you don't want to use that model? Fine. Don't use Diminuto in that particular instance. There's nothing keeping you from coding to the native Linux or GNU API. Hey, knock yourself out. You can still make use of the Diminuto log facility. You can make your own horrifically tragic mistakes. In these here parts, we call that a learning experience.

Layer 8: Functional Tests

Besides unit tests, Diminuto also includes a host of functional tests. These form the last line of defense against some boneheaded blunder on my part. They also provide, along with Diminuto's unit tests and command line tools, some really useful examples (I use them myself) of how to use Diminuto in the real world.

Some of the functional tests use special test fixtures I fabricated just for this purpose, to test hardware-centric features like General Purpose Input/Output (GPIO) pin input and output, serial port reading and writing, and pulse width modulation (PWM).

When I make a change to any of this hardware-related code, or its dependencies, or just when I'm feeling lonely, I get the text fixture out, hook everything up, and run some functional tests that do things like light up LEDs in response to button presses, or adjust the illumination of an LED to achieve some specific value of lux on a light sensor.

The functional tests and command line tools form the outermost layer of the Diminuto framework.

End Matter

Diminuto has been enormously useful to me (and, sometimes, to my clients) for a wide variety of reasons, not the least of which are the lessons I carried away from the layered architecture which emerged organically from its development.

If you want to see non-trivial examples of Diminuto in action, checkout the gpstool and rtktool applications that are part of my Hazer GPS/GNSS project. They each make good use of a variety of Diminuto features. gpstool, rtktool, and their Diminuto underpinnings, are in constant use, 24x7, as part of my Differential GNSS work.

Supporting Material

Chip Overclock, "Being Evidence-Based Using the sizeof Operator", 2015-03, <https://coverclock.blogspot.com/2015/03/being-evidence-based-using-sizeof.html>

Chip Overclock, "Buried Treasure", 2017-01, <https://coverclock.blogspot.com/2017/01/buried-treasure.html>

Chip Overclock, "Some Stuff That Has Worked For Me In C", 2017-04, <https://coverclock.blogspot.com/2017/04/some-stuff-that-has-worked-for-me-in-c.html>

Chip Overclock, "renameat2(2)", 2018-04, <https://coverclock.blogspot.com/2018/04/renameat22.html>

Chip Overclock, "When The Silicon Meets The Road", 2018-07, <https://coverclock.blogspot.com/2018/07/when-silicon-meets-road.html>

Chip Overclock, "When Learning By Doing Goes To Eleven", 2020-03, <https://coverclock.blogspot.com/2020/03/when-learning-by-doing-goes-to-eleven.html>

Chip Overclock, "Headless", 2020-06, <https://coverclock.blogspot.com/2020/06/headless.html>

Chip Overclock, "Clock Time", 2020-10, <https://coverclock.blogspot.com/2020/10/clock-time.html>

Chip Overclock, "Timer Threads", 2020-10, <https://coverclock.blogspot.com/2020/10/timer-threads.html>

Afterword (updated 2020-11-19)

This afterword got so long I promoted it to its own blog article: Is the Virtuous Cycle really that virtuous?