Tick

I've decided that I might as well accept the Buddhist view of time: that time itself is an illusion and our conception of it is merely a measure. The only way we have to perceive time is in the relative order of events that take place, regardless whether time somehow exists independently of these events or not. All timekeeping ultimately depends on a frequency source - or oscillator - which is nothing but a generator of evenly spaced events. The number of events generated per second is the frequency of the oscillator, and is measured in Hertz.

Update 2021-10-23: While engineers and scientists conventionally measure the frequency of an oscillator in Hertz (Hz), also known as cycles per second, mechanical watch designers and aficionados typically measure in vibrations per hour (VPH) or beats per hour (BPH). I recently learned that while Hertz counts a complete back-and-forth movement, or cycle, of the mechanical part (think of a pendulum), which is a complete tick tock sequence, the vibration or beat considers the tick and tock separately. So an oscillator with a frequency of 4 Hz can be said to beat at 28,000 VPH or BPH. [Ref: Logan Baker, "What Does Watch Frequency Mean?", Hodinkee, 2021-08-21]

(Clock with a 4Hz oscillator using a pendulum resonator and a deadbeat escapement.)

Every oscillator makes use of a resonator, some source of periodicity that we take from nature: the motion of the sun, the fall of a drop of water, the swing of a pendulum, the rotation of a balance wheel, the vibration of a quartz crystal, the hyperfine transition of a cesium atom. If something happens faster than the interval between the beats of that oscillator, the only way to measure that interval is to use an oscillator with a higher frequency, which may mean a different resonator: the transition of an aluminum atom or of a ytterbium atom. How do we use these oscillators? By treating each beat of the oscillator as an event, and counting the number of events that occur during the time interval we want to measure.

(Watch with a 6Hz oscillator using a balance wheel resonator and a lever escapement.)

Is there a maximum possible frequency? Physicists think so: the reciprocal of one Planck time, which is about 5.39 x 10^-44 seconds. It's the amount of time it takes a photon to cross a Planck length. One Planck time is the shortest time interval physicists believe can meaningfully occur, the duration it takes for the fastest possible object to cover the shortest possible distance found in nature. My calculator tells me that such a hypothetical Planck-frequency oscillator beats at a frequency of about 1.85 x 10⁴³ Hertz. That's a lot of Hertz.

(Slow motion deadbeat escapement creating the tick tock.)

What happens between the beats of this hypothetical Planck-frequency oscillator? The question has no meaning; we believe one Planck time is the smallest possible interval that can occur. Time might as well not exist between the beats of a Planck-frequency oscillator. If we want to talk about the time between any two events, we have to find a frequency source that generates events more frequently than the interval we want to measure - any other notion of time is purely an abstract concept - and there is nothing faster than a Planck-frequency oscillator. (I'm told there may actually be even shorter time intervals in the field of quantum gravity, but they are apparently impossible to measure; what this might mean is left as an exercise to the reader.)

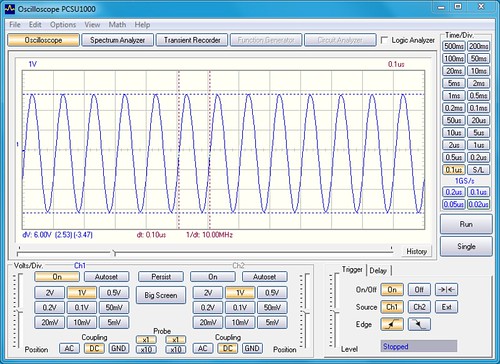
(Snapshot of an oscilloscope on a 10MHz oscillator with a cesium atomic resonator.)

I didn't come to this notion by reading about the more esoteric aspects of physics (as much as I enjoy doing that). I did it by developing and debugging real-time firmware that shaped the emission rate of ATM cells on a SONET channel carried over an OC-3 optical fiber. By building a stratum-0 NTP server with a cesium reference oscillator. By assembling an educational model of a mechanical clock.

(Ytterbium lattice optical atomic clock at the NIST Boulder Labs.)

Update 2021-10-23: Remarkably, not long ago, I changed my mind, after considering how General Relativity and Special Relativity affects our measurement of time. The former causes time to speed up the further we are from the gravitational influence of a mass, and the latter causes time to slow down the faster we go. These are real measurable effects that systems like the Global Positioning System (GPS) that depend on timekeeping have to take into account. The GPS satellites are in orbit at 20,000 km, so their atomic clocks are further away from the mass of the Earth than those on the surface. This causes them to run faster by about 45 microseconds a day when compared to atomic clocks on the ground at sea level. But the satellites are also moving at 14,000 km/hour. That centripetal acceleration causes them to run slower by about 7 microseconds a day. This requires a net adjustment of 38 microseconds per day relative to clocks on the ground. Whatever time is, it is a real thing, the measurement of which can be affected by physical events and circumstances. [Ref: Richard W. Pogge, Real-World Relativity: the GPS Navigation System, The Ohio State University, 2017-03-11]