More Is Better
When your GPS receiver calculates the range to a GPS satellite, we tend visualize that computation as the receiver resting somewhere on a sphere defined by the space vehicle at the center and the radius being the range. The receiver doesn't know where on the sphere it resides. But all points on that sphere are equidistant from the satellite.

But that visualization doesn't really capture the reality of the situation. Because there is inevitably some variation or jitter in the timing of the signal from the satellite, the situation is more accurately visualized as a sphere within a sphere. The two spheres represent the minimum and maximum value of the range given its uncertainty. Your receiver is somewhere in the volume that is the interstitial space between the two spheres.
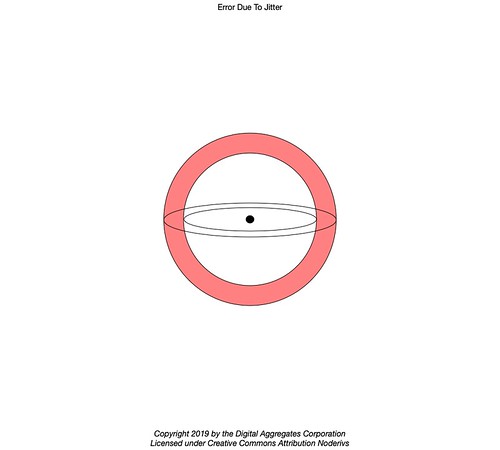
We continue to mislead ourselves by visualizing the range to a second satellite defining a second sphere which intersect with the first in a circle.
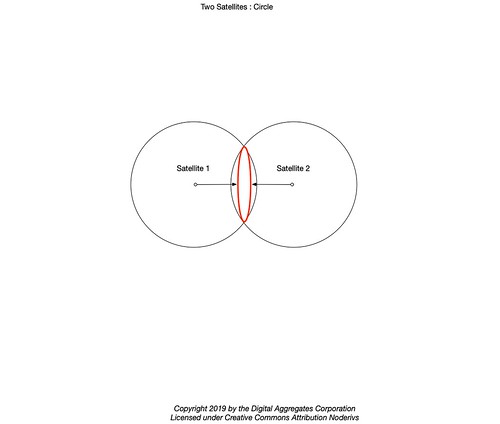
But this is also incorrect. What actually happens is a second set of two nested spheres intersects with the first, reducing the volume in which the solution of the position fix may reside into the shape of a doughnut or a pancake depending on how much they overlap.

The addition of more computed ranges from more satellites keeps chopping away at this volume, as the solution lies in the intersection of all the volumes of the individual solution spaces.
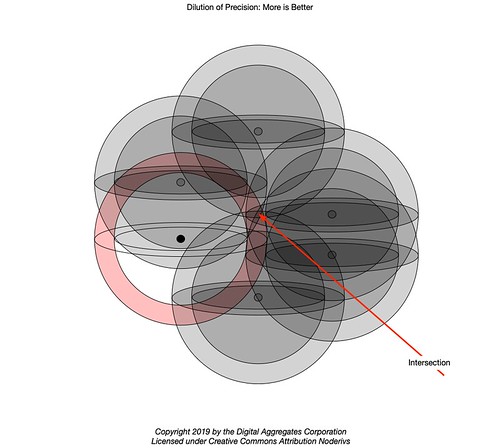
This is definitely a case of More Is Better. As in: more than the four, and only four, satellites needed for the closed-form algebraic multilateration algorithm. So modern GPS receivers - like yours - instead use an iterative approach based on the least squares algorithm, handy when a problem is overdetermined: more equations (computed ranges) than free variables (X, Y, Z, and T).
Your GPS receiver feeds the algorithm as many ranges as it can compute from the satellites in view. The receiver is also tasked with synchronizing its internal clock to GPS Time, solving for X, Y and Z , its position in space, as it adjusts T. Until this is done, the computed ranges cannot be accurate. In fact, they will each be off by a billion feet for every second the internal clock differs from the time on the synchronized atomic clocks in the GPS constellation.
So the processor in your GPS receiver iterates by adjusting its clock in whatever direction causes this computation to converge. This is in whatever direction causes the intersected volume defined by the range spheres to grow smaller, with the goal to draw the spheres to intersect at a point. Eventually the volume is reduced, probably not not to zero, but to some value of T in which any additional change causes the volume to begin to grow again as the spheres move apart.
At this point, three really useful things have occurred.
First: your GPS receiver now knows its position within a volume. It's not perfect, but it's as good as it's going to get.
Second: your GPS receiver has a measure of the accuracy of its solution, in terms of the size of the minimized solution volume bounded by how far apart the range spheres are. This is a useful thing to know.
Third: your GPS receiver's internal clock is now, and continuously as long as position fixes keep coming, closely synchronized to GPS Time. This makes subsequent position fixes much faster. Should your receiver loose contact with the GPS constellation - for example, your automobile drives under an overpass (short time) or into a tunnel (long time) - whether the algorithm has to start from scratch when the GPS signals are reacquired depends on how long it was cut off and the quality of its internal clock (holdover). But even if it has drifted some relative to GPS Time, if it has not drifted much, subsequent position fixes will be must faster.
But this iterative, geometric, approach to achieving a position fix has its own issues.
Dilution Of Precision
Not all satellites are created equal. Considering the two satellite diagram above, we think of the overlap between the two solution spaces as being relatively small compared to the volumes in the two sets of nested spheres individually.
But that assumes that the satellites used for the position fix have wide physical separation. This requires a very broad view of the sky (as shown in the diagram) so that your GPS receiver can use satellites whose orbits have not placed them close together.
What if the your GPS receiver is in a canyon, perhaps an "urban canyon" between two ginormous buildings, so that it has a restricted view of the sky?
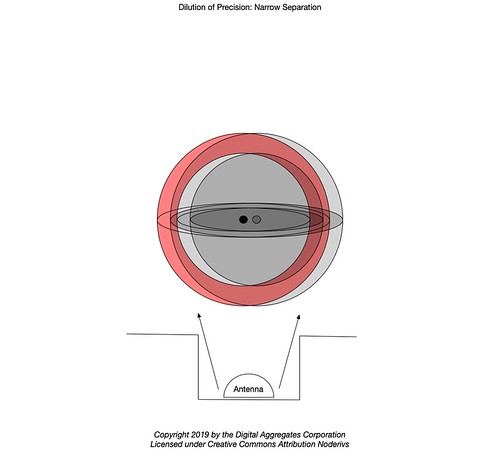
In this case, the overlap of the two solution spaces may be nearly 100%, because your receiver can only see satellites whose orbits happen to place them very close together, in that narrow slice of sky, at the time of the position fix. The addition of a second satellite does not do much to reduce the volume in which the position fix may reside. As we continue to add more ranges to the algorithm based on satellites in close proximity, the final position fix volume may still be quite large.
This is called Dilution Of Precision (DOP). DOP measures how sensitive the position solution (output) is relative to changes in the pseudo-ranges (input). The closer the satellites are in their respective orbits, the less sensitive the solution is to their movement. Less sensitivity is a bad thing. DOP is an artifact of the geometry of the satellites your GPS receiver chose to use as part of its position fix. Your GPS receiver may compute and display a DOP value (or maybe several different DOP values, for both horizontal and vertical position) based on its assessment of the geometry of the GPS satellites it was able to use in its computation. The DOP value will be a number ranging from ~1 (excellent) to >20 (Timmy has fallen down a well with his GPS receiver).
In the testing I've been doing lately, I have seen DOP values ranging from 0.93 (pretty sure I know where I am) to 5.74 (just okay), depending on the antenna I was using and its view of the sky.Your GPS receiver examines its received almanac of satellites and chooses those with the widest geometric separation for its position fix. But this isn't as easy as it sounds: at most six GPS satellites will be in view at any one time, and in most circumstances this is optimistic. A minimum of four are needed for a position fix. More is better. Which leads us to the next approach to improve position fixes: using more satellite constellations.
It occurred to me that an optimization would be to use the closed-form algebraic solution using the four most widely separated satellites to get initial values of X, Y, Z and T, set the internal clock, than use as many satellites as the GPS receiver could muster to iterate from that starting point. This would be especially useful after broadening the number of available satellites using the approach described below.GNSS
Until a couple of years ago, all of the GPS receivers I tested were designed to only receive signals from the U.S. GPS constellation. That makes sense: until less than a decade ago, GPS was the only satellite navigation system with global coverage.
In 2011, in what is said to be the most expensive program it has ever untaken, the Russian Federation completed its GLObal Navigation Satellite System (GLONASS), adding a second satellite navigation system with global coverage to the world.
A few years ago I began to find reasonably priced GPS receivers that worked with both GPS and GLONASS, choosing amongst the satellites from both constellations for position fixes.In 2016, the European Union completed its own satellite navigation system with global coverage when Galileo went live.
In 2018, Beidou ("Northern Dipper"), a satellite navigation system developed by the People's Republic of China, began providing global coverage. Beidou (or, sometimes, COMPASS) is expected to be completed by summer of 2020.
The latest GPS receivers I've been experimenting with support GPS, GLONASS, Galileo, and Beidou, providing they are used with a multi band antenna capable of receiving the different frequencies used by each system. The receivers choose individual satellites amongst all four constellations to achieve the most accurate position fixes. Some of the these receivers can occasionally make simultaneous use of thirty-two satellites for position fixes, the limit of their particular hardware.It is for this reason that I now use the more generic term Global Navigation Satellite Systems (GNSS) instead of GPS, since my work routinely encompasses all four constellations.
This might be a good time to note that like GPS, the other GNSS constellations are considered strategic assets which are under control of organizations that might turn them off or otherwise deny their public, civilian use at any time. This is another case of More Is Better, since using multiple systems not only provides more accuracy, but they serve as backups for one another. I might note also that the EU system, Galileo, has suffered a couple of shocking technical failures, one of which took it out of service for an entire week, and which my own systems noticed before it appeared in the news. The U.S. military from time to time announces that it is going to test GPS jamming at White Sands Missile Range in New Mexico, and my simple consumer equipment has noticed the effects from this near Denver Colorado.Still not good enough?
There are still more ways to achieve better accuracy when using GNSS.
This screen snapshot is part of my Differential GNSS project. (Click on it to see a larger size.) This fixed base station is sending corrections over the internet to mobile rovers. Both the base and the rovers are using u-blox ZED-F9P GNSS modules.

The base is currently computing its position fix using twenty-five different satellites distributed across all four constellations. (And at some time in the past it was able to use thirty-two satellites.) It self-reports a horizontal accuracy of ±0.0204 meters (a little less than an inch) and a vertical accuracy of ±0.0144 meters (a little over half an inch). It is not computing DOP values (hence the 99.99 place holders).
That will be a topic for another article.

No comments:
Post a Comment