In this article I'll explain, at least at my dilettante level of knowledge, how GPS works.
Satellites
In 1978, the U.S. Department of Defense launched the first satellite that was part of the Navigation System using Timing And Ranging (NAVSTAR) Global Positioning System (GPS). Today, there are thirty-one active satellites that make up the constellation that we now refer to as just GPS. In addition, there are nine backup satellites, two of the next (third) generation of GPS satellites being tested, and thirty older satellites that have been retired.

This is actually a pretty good Lego model I built of a Block IIF GPS satellite, complete with solar panels and antenna. To give you a sense of scale, the main body or bus of the actual space vehicle, the part here in yellow that represents the gold foil on the real thing, is over eight feet high. So the real vehicle is a substantial piece of kit.
Like all the images in this article, you can click on it to see a larger version.

Some of the antennas have nothing to do with GPS. As far as I know, all current GPS satellites still serve a dual mission in that they carry instruments to detect nuclear testing.
This might be a good point to remind ourselves that GPS is a military system under the purview of the U.S. Department of Defense. GPS satellites may have other, classified, missions. And the U.S. DoD can test, interfere, or even disable the system, should circumstances warrant. During my own testing I have had my GPS equipment near Denver Colorado temporarily disabled by GPS jamming as part of an announced test at White Sands Missile Range in New Mexico. The vital military and civilian importance of the GPS function also makes these satellites potential targets of foreign adversaries.The satellites are unequally distributed into six different orbital planes. The orbital planes, and the satellites within each of them, are arranged such that from anywhere on earth, given an unobstructed view of the sky, at least six satellites should be in view at any one time.

The orbital planes do not exactly match the struts along the circumference of a Hoberman Sphere (reserving one circumference for the Earth's equator), but they are close enough that I felt compelled to buy one at my local toy store to use in talks. It's a useful tool to visualize what the orbital planes look like.
Each satellite is at an altitude of more than 20,000 kilometers or about 12,500 miles when it is directly overhead. That's classified as a Medium Earth Orbit (MEO). It takes each GPS satellite just a smidge under twelve hours to complete an orbit and arrive back over the same point on the Earth.
Satellites have a limited life span. Not only do components fail, but they require frequent repositioning using on-board rocket motors to adjust their orbits; eventually a satellite runs out of fuel. That's one of the reasons why some of the GPS satellites in orbit are not used.
Signals
Each GPS satellite broadcasts on more than one radio frequency, all in the microwave region, not all of which are decodable by GPS receivers available to civilians. But for the frequency that is available to the GPS receiver you and I can purchase at the local camping store, all of the satellites transmit on that same frequency, all the time, using a multiplexing technique called Code-Division Multiple Access (CDMA), a technology that originated in the telecommunications industry for cellular phones.
Even though the GPS satellites all transmit on the same frequency at the same time, the signals all mixing with one another, your GPS receiver is able to discriminate the data stream from each individual satellite using a sophisticated decoding algorithm. Each individual satellite uses a unique binary key, or Gold Code, with which to encode its data stream. The GPS receiver knows the unique key used by each satellite - in fact, the specific Gold Code effectively identifies the satellite from which the data stream originated - and it uses that key to decode the data stream. In other applications, many devices all transmitting on the same frequency would result in a jumbled mess. But a GPS receiver can receive and decode data from many GPS satellites simultaneously.
Mobile telephone service providers, like Verizon Wireless, use this same CDMA technology, albeit on different frequencies than GPS. Equipment at the cell phone tower decodes the individual data streams from many mobile devices, all speaking on the same frequency simultaneously. The first time I learned how this worked in a seminar I was taking - I was working on software and firmware for cellular base stations at the time - I thought: This is impossible! But clearly it is not.Each GPS satellite transmits with a power of about forty-five watts. That's less than a typical old fashioned incandescent light bulb. Your GPS receiver does a remarkable job of amplification and signal processing to extract the data stream from the GPS satellites overhead, who can barely be said to be whispering to it from afar.
The use of CDMA makes for efficient use of radio frequency spectrum. Unfortunately, it also makes it easy to jam such applications, whether they be GPS or mobile phones. A jammer merely has to transmit random noise on the appropriate frequency and at relatively low power to defeat the decoding algorithm. GPS jammers which are highly illegal are devices that can fit in the palm of your hand and be powered by the lighter socket in an automobile. This is why jamming GPS signals is trivial. GPS receivers can also be spoofed by more powerful transmitters, causing them to compute the wrong position.
Positioning
Your GPS receiver uses a technique called pseudorange multilateration to determine its position relative to the GPS satellites whose signals it can receive.
Each GPS satellite has several atomic clocks, cesium or rubidium, for redundancy. These clocks are all synchronized to one another, and in turn to all the clocks in all the other GPS satellites, and ultimately to a master atomic clock at the GPS master control center near Colorado Springs, Colorado. The time to which these clocks are synchronized is referred to as GPS Time.
If you are into to this sort of thing (which, long time readers will realize, I am), GPS Time isn't quite International Atomic Time (TAI), nor is it Universal Coordinated Time (UTC). TAI has no leap seconds. UTC has lots of leap seconds, and gets another one every few years to adjust it to changes in the Earth's slowing rate of spin. GPS Time is somewhere in between, having adopted however many leap seconds UTC had at the time the GPS system was first established.
Your GPS receiver has a clock in it - not an atomic clock, and in fact probably not much better than the watch you may wear on your wrist - that is synchronized to GPS Time. (We'll get to how that's done momentarily.)
Your GPS receiver knows the orbits, or ephemerides, of all the satellites in the GPS constellation to a very high degree of accuracy. (We'll also get to that shortly.)
Your GPS receiver knows the speed of light. So when it receives a data frame from a GPS satellite that contains a timestamp indicating when it was transmitted, your receiver can calculate how long it took for that frame to travel from the satellite to itself. Given the speed of light, your GPS receiver can compute the distance, or range, between it and the satellite.
The term pseudorange is used to remind us that the range calculation is at best an estimate, and may in fact be inaccurate for all sorts of reasons, not the least of which is that the internal clock of the GPS receiver is not (yet) synchronized with the clocks in each of the satellites whose signals it has received. (We'll discuss some of the other reasons later.)

Because your GPS receiver knows the ephemeris of that satellite - it knows the satellite's position to a high degree of accuracy when the frame was transmitted, and later, when it was received - the receiver knows it must be somewhere on the surface a sphere in which the GPS satellite is in the center, the radius of the sphere being the range to the satellite. It doesn't know where it is on this sphere, but it has to be somewhere on its surface for that range to be correct.
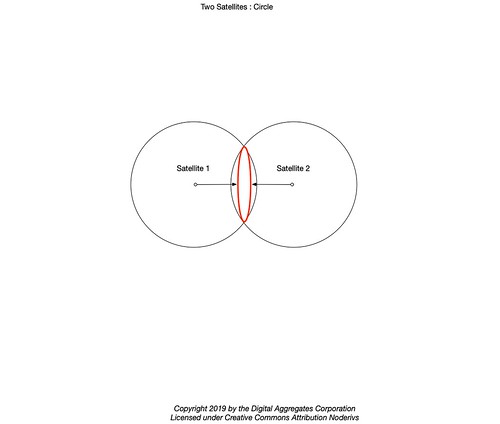
Your GPS receiver makes the same calculation for another frame it received at the same time from a second satellite. This creates a second sphere that intersects with the first sphere. The intersection of two spheres is a circle (or, in the degenerate case where the two spheres are barely touching, a point).

A third satellite produces a third sphere. The intersection of that third sphere with the circle produces two points. Since the ephemerides of the GPS satellites describe their orbits in space, these spheres are quite large. One of those points will be on or near the surface of the Earth, and the other point will be out in space.

A fourth satellite yields a fourth sphere, which will intersect with the just one of those two points. That point is the position of your GPS receiver at the time it received the frames from each of the four satellites.
Your GPS receiver is continuously receiving frames from all of the GPS satellites it can see at the time, and computing a solution to its position. A typical GPS receiver computes a new solution or fix once a second. GPS receivers used in aircraft or other high speed vehicles may compute a solution more often, perhaps five or even ten times a second. By comparing successive solutions and the times they were computed, a GPS receiver can establish its velocity or Speed Over Ground (SOG), and its heading or Course Over Ground (COG).
But of course, it's not quite that simple, as we'll see below, where I'll also try to resolve some of the questions I left unanswered.
Details
The bit rate of GPS transmissions is quite low: fifty bits/second. GPS navigation messages are divided up into 1500 bit frames, and each frame is divided up into subframes. The navigation message contains the time and date of its transmission plus the information described below.
Each GPS satellite periodically transmits its own ephemeris, a high precision description of its orbit. Every satellite also transmits an almanac, which contains a low precision description of the orbits of every satellite in the GPS constellation. The almanac also includes the state of health of each satellite; GPS satellites are sometimes temporarily removed from service for maintenance or even retired completely. The almanac lets your GPS receiver know which satellites it can expect to be in view and receive from at any one time. It is the ephemeris for each satellite that allows the receiver to calculate its range to that satellite. Both the almanac and the ephemerides are updated periodically by GPS ground control.
It takes 12.5 minutes for any one GPS satellite to transmit the entire almanac, providing the signal from the satellite to your GPS receiver is stable long enough that the GPS receiver sees all of the frames in the multi-frame sequence that carries the complete almanac. The receiver caches the most recent almanac (and maybe the ephemerides) that it has received. Some receivers even have non-volatile memory with which to store this information across power cycles. The almanac and ephemerides change often enough that the receiver has to age the information out of the cache if it is too old.
When a receiver has cached information that it believes is valid, it can do a warm start. This can make a big difference in the Time To First Fix (TTFF). Otherwise it must do a cold start, and wait to receive the entire almanac, and then the ephemeris for each satellite in view.
Just recently I had a receiver take twenty-three minutes TTFF during a cold start. This is not that unusual.
(Update 2021-09-08: I have also seen some newer GPS receivers compute an initial fix in as little as a minute after a cold start. This is truly impressive, since there is no way they could have had the almanac - verified by the fact that during this first minute the satellites they report in view indicate no azimuth or elevation. According to their documentation, these receivers are devoting a relatively vast number of radio channel resources to brute force scan for satellites and then using the individual ephemeris that each satellite transmits every thirty seconds. That such GPS devices are able to do this is truly a result of Moore's Law in action. My first GPS receiver - an expensive dedicated handheld unit I bought many years ago - had a single radio channel. Today I have a recent inexpensive GPS receiver with seventy-two channels.)When you first turn your GPS receiver on, it's clock will probably not be synchronized to GPS Time. Even if you could set the clock, you could not set it to the precision necessary for GPS. A useful rule of thumb is that light travels about a foot in a nanosecond. So for every nanosecond the clock in your GPS receiver differs from GPS Time, every range it calculates will be off by a foot or more. If your clock is off by a full second, ranges will be off by at least a billion feet. That's a lot of feet.
Your GPS receiver addresses this problem by solving not only for its own X, Y, and Z position in space using multilateration, but for its position T in time. There exists a closed form algebraic solution for X, Y, Z, and T using ranges to just four satellites. What's remarkable about this is that not only does this give you a solution for your position in space, but as a side effect it continuously synchronizes the clock in your GPS receiver to GPS Time, making your GPS receiver the most accurate clock you will probably ever own.
Your mobile phone may do this as well, but it is more likely to synchronize its clock to the Network Time of its mobile service provider, who in turn synchronizes that to GPS Time. Every cellular base station typically has a rubidium atomic clock that is disciplined by its own GPS receiver just for this purpose. Mobile telephone networks - and lots of other applications as well - depend on GPS as an accurate frequency source for precision timekeeping. The higher the frequency - and hence the larger the bandwidth - of a mobile network, the more important this is.Like many cryptological algorithms, your GPS receiver is considered a munition under the definitions in the U. S. Department of State International Traffic in Arms Regulations (ITAR), sometimes referred to under it's earlier title as the Coordinating Committee for Multilateral Export Controls (COCOM). It is for this reason that civilian GPS receivers have built-in COCOM Limits that prevent them from working if they calculate that they are moving faster than 1000 nautical miles per hour (knots), equivalent to 1900 kilometers/hour or 1200 miles/hour, or at an altitude above 18,000 meters or 59,000 feet. This is to prevent you from building your own cruise missile in your basement.
As a software developer, I never anticipated I'd be sitting in my cubical reading ITAR regulations to figure out whether we would be violating the law by shipping a GPS application in an embedded system which could be installed in business aircraft with the range to fly to China. That's just one more thing that makes my job interesting.However, these restrictions have an unexpected useful side effect in that one of the two possible solution points mentioned above for the three sphere case, the one far out in space, can be trivially eliminated. Unless of course you are using a specially licensed GPS receiver on the International Space Station. Or on a deep space probe. Both of which actually totally happen. In which case you are sitting above the GPS satellite constellation instead of below it, and are depending on very faint signals arriving from lobes of the GPS signals peeking out around the edges of the Earth in whose GPS signal shadow you sit.
Current GPS satellites aim their signals down towards the surface of the Earth. There is some discussion about future generations of GPS satellites transmitting their signals in all directions, to make them more useful for navigation in our solar system. That would be cool.
(Update 2021-09-08: Point of clarification: it is this optimization in which your terrestrial GPS receiver assumes it is near the Earth and not out in space that allows it to compute X, Y, Z, and T with only four satellites. If you had a receiver exempt from the ITAR/COCOM restrictions that made no such assumption, it would require five satellites for its initial position fix: four for the spatial solution and one more for the time solution.)
But there are lots of other sources of error, like when the received GPS signals are reflected off an object like a building, vehicle, or tree cover, adding variable latency to their computed arrival times. The ionosphere itself adds variable latency to the signals, and the angle of the signal path or even weather effects can increase or decrease this error. Some information about atmospheric conditions are actually part of the data carried in one of the GPS frames.
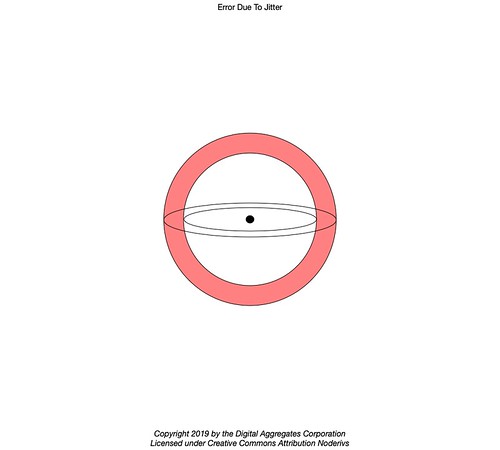
Because errors in the timing of the signals from each of the GPS satellites is a given, the cleanly intersecting spheres described above do not exactly reflect reality. Each sphere that is the result of a range calculation to a particular satellite isn't a sphere at all, but a sphere within a sphere, representing the error bars of the calculation. The position fix can be better thought of resting then, not on a sphere, but somewhere in the space between the two nested spheres representing the plus or minus error in the timing of the signal.
That will be a topic for another article.

No comments:
Post a Comment