Location, Location, Location

That's the punch line for the old joke: "What's the three most important factors in determining the desirability of a piece of real estate?" It's also the answer to "What's the three most important factors that affect precision and accuracy when using Global Navigation Satellite Systems?" It turns out that antenna placement is critical, with antenna selection running a distant second.

The data I'm going to present are not the results of careful controlled experiments. They are derived from datasets I already had lying around that I collected while testing Tumbleweed, my Differential GNSS project. But the data exposes what really matters. Some of this data has already appeared in my prior article Negative Results Are Still Results. In Dilution of Precision I explain how a poor view of the sky both limits the number of satellites your receiver's algorithm can use in its iterative solution, and its flexibility in choosing amongst those satellites to find the ones with the widest orbital separation.  More is better.

For all of these examples, I'll be using two metrics: the diameter of the smallest circle that can drawn around all of the positioning solutions gathered over time (using my tools csvlimits and geodesic), and a visualization of the positioning solutions achieved by converting the CSV output of my software into a Keyhole Markup Language (KML) file and imported it into Google Earth (using my tool csv2kml).

(2020-06-03: This article has been edited to append an additional example at the end.)

Location: NGS KK1446



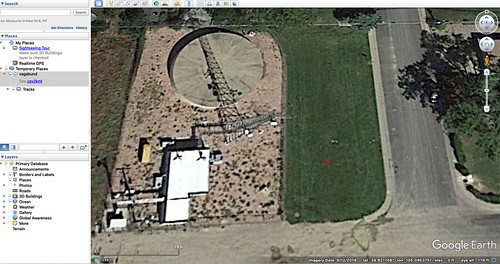
This used a survey-grade multi-band GNSS antenna (the white saucer-shaped object on top of the tripod) purchased from Ardusimple with the u-blox ZED-F9P GNSS module with my software running on a Raspberry Pi 3B+. The site was an open field containing NGS survey marker KK1446. The view of the sky was excellent. This combination allowed the receiver to use as many as twenty-nine satellites from four different constellations for its solution.

Uncorrected: 0.6925 meters



Corrected: 0.0423 meters



The combination of a survey-grade multi-band antenna with the nearly perfect view of the sky gives an excellent showing. The use of differential corrections reduces the diameter of the solution circle from about 0.7 meters to just about four and a quarter centimeters, a factor of more than sixteen improvement. The corrected view from Google Earth has red marks so small that you need to click on the image to see it in the larger version.

Location: Second Story Window



This used a multi-band GNSS antenna (far left) purchased from Ardusimple with the u-blox ZED-F9P GNSS module with my software running on a Raspberry Pi 3B+. The antenna no longer appears in their catalog, and has no markings on it; but from its weight and dimensions, I believe it has a built-in ground plane (a good thing). The site is a south-facing second-story window in my home office. The view of the sky is fair: only the southern half of the sky is visible, but that part is mostly unobstructed. Even with this partial view, the receiver was able to see as many as twenty-six satellites from four different constellations.

Uncorrected: 5.1404 meters



Corrected: 2.3099 meters



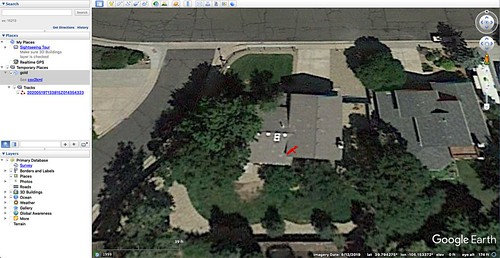
The use of differential corrections reduces the diameter of the solution circle from about five meters to about two and a quarter meters, a factor of about two. This illustrates how differential correction can only do just so much. The uncorrected diameter is very typical of consumer GNSS receivers with their integral patch antennas and a good view of the sky.

Location: Lab Bench



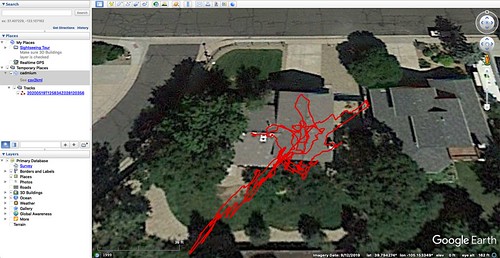
This used a multi-band GNSS antenna purchased from Ardusimple with the u-blox ZED-F9P GNSS module with my software running on an Intel i7-class system. The antenna - the small black vertical cylinder attached directly to an Ardusimple SimpleRTK2B board in a 3D-printed case - is a helical antenna intended for applications like aerial drones, its principle advantages being its light weight and its relative insensitivity to orientation. In my application, the antenna picked up only two of the four GNSS constellations, GPS and GLONASS, during the test period, despite being advertised to pick up all four. The site is the lab bench that sits on the opposite side of my home office, a little over two meters from the same window as above. The view of the sky is poor. Typically only four or five satellites from the two constellations are visible, for example, three GPS, two GLONASS; had this not been a multi-band antenna, it would not have been able to make a position fix using the minimum of four satellites.

Uncorrected: 37.5433 meters



Corrected: 68.2234 meters



You are not imagining this: the uncorrected test run was better than the corrected test run. (I was so skeptical myself that I triple checked that I hadn't gotten the datasets confused.) Neither were worth writing home about. Some of the data points from on the corrected test blew clean over my home to the lot to the east, and even to the lot east of that. This test setup is adequate for regression testing my software for basic functionality, but in no way yields actually useful positioning except at very coarse granularity.

Location: Second Story Window (added 2020-06-03)



This is a later test in which I took the same helical multi-band GNSS antenna (on the left) and tested it in the same location as and alongside the prior setup (which used the antenna on the right) in the south-facing home office window. As before, it uses the Ardusimple SimpleRTK2B board with the u-blox ZED-F9P module, although in this case the Linux/GNU host running my software was an ancient H-P Mini 110 netbook with an Intel i686-class processor. (The u-blox module does all the heavy lifting; my software merely runs the real-time display and collects the data.)

Uncorrected: 3.4650 meters



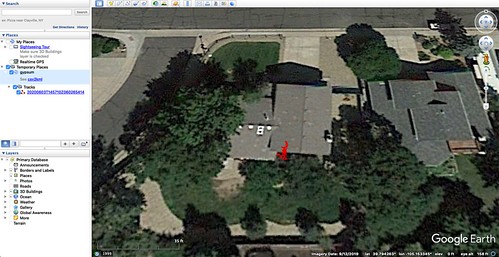
Merely moving the helical antenna a couple of meters or so from the lab bench to the window makes a huge difference. In fact, in this one instance the small light helical antenna slightly outperformed the larger antenna from the prior test. Moving the antenna to a better view of the sky also allowed it to use as many as twenty-five satellites from all four constellations, versus the barely minimally adequate five satellites from two constellations. The solution diameter of 3.465 meters - over eleven feet - still illustrates how coarse the resolution of uncorrected GNSS is. An aerial drone using this configuration and seeing this kind of resolution would find autonomous navigation problematic.

Location, Location, Location

Differential GNSS can make a big difference, and antenna selection is important. But unless you have proper antenna placement, neither a good antenna nor differential corrections are going to save you.